Two sides of a triangle have lengths 4 and 10. If the third side has a length of integer x, how many possible value are there for x?
The correct Answer is:Seven
To determine how many possible integer values the third side x of a triangle can take, given the lengths of the other two sides are 4 and 10, we can follow these steps:
Step 1: Apply the Triangle Inequality Theorem
The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Step 2: Set Up the Inequalities
For our triangle with sides s1=4, s2=10, and s3=x, we can set up the following inequalities based on the theorem:
1. s1+s2>s3
2. s1+s3>s2
3. s2+s3>s1
Step 3: Solve Each Inequality
1. From 4+10>x:
14>xorx<14
2. From 4+x>10:
x>10−4⇒x>6
3. From 10+x>4:
x>4−10⇒x>−6(This inequality is always true since x is positive)
Step 4: Combine the Results
From the inequalities, we have:
- x<14
- x>6
Thus, we can combine these results to get:
6<x<14
Step 5: Determine Possible Integer Values
The integer values that satisfy 6<x<14 are:
- 7, 8, 9, 10, 11, 12, 13
Step 6: Count the Possible Values
The possible integer values for x are 7, 8, 9, 10, 11, 12, and 13. This gives us a total of 7 possible values.
Final Answer
The number of possible integer values for x is 7.
---
The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
For our triangle with sides s1=4, s2=10, and s3=x, we can set up the following inequalities based on the theorem:
2. s1+s3>s2
3. s2+s3>s1
1. From 4+10>x:
14>xorx<14
x>10−4⇒x>6
x>4−10⇒x>−6(This inequality is always true since x is positive)
From the inequalities, we have:
- x<14
- x>6
6<x<14
The integer values that satisfy 6<x<14 are:
- 7, 8, 9, 10, 11, 12, 13
The possible integer values for x are 7, 8, 9, 10, 11, 12, and 13. This gives us a total of 7 possible values.
The number of possible integer values for x is 7.
Similar Questions
Knowledge Check
- Question 1 - Select One
Two sides of a triangle measure 4 and 12. Which of the following could equal the length of the third side?
A5B7C9D20
Two sides of a triangle are 4 cm and 10 cm. what is the possible range of length of the third side ?
View SolutionIf two sides of a tringle are of length 5 cm and 1.5 cm, then the length of third side of the triangle cannot be
View SolutionTwo sides of a triangles are 12 cm and 7 cm , find the range for the length of its third side.
View SolutionFind the length of the third side of the triangle.
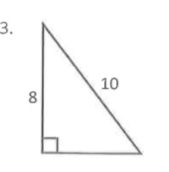 View Solution
View SolutionFind the length of the third side of the triangle.
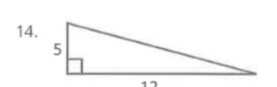 View Solution
View SolutionIf two sides of a triangle are ˆi+2ˆjandˆi+ˆk, then find the length of the third side.
View SolutionTwo sides of a triangle are of lengths √6and4 and the angle opposite to smaller side is 30. How many such triangles are possible? Find the length of their third side and area.
View Solution

