Two sides of a triangle are of lengths √6and4 and the angle opposite to smaller side is 30. How many such triangles are possible? Find the length of their third side and area.
Step by step video & image solution for Two sides of a triangle are of lengths sqrt6 and 4 and the angle opposite to smaller side is 30. How many such triangles are possible? Find the length of their third side and area. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Two sides of a triangle are of lengths √6and4 and the angle opposite to smaller side is 30. How many such triangles are possible? Find the length of their third side and area.
View SolutionTwo sides of a triangle are of lengths √6and4 and the angle opposite to smaller side is 30. How many such triangles are possible? Find the length of their third side and area.
View Solution
Knowledge Check
Two sides of a triangle are of length 4 cm and 10 cm. If the length of the third side is a cm, then
Aa>5B6≤a≤12Ca<6D6<a<14Two sides of a triangle are 2√2and2√3cm and the angle opposite to the shorter side of the two is π4. The largest possible length of the third side is
A(√6+√2)cmB(√6+√2)cmC(√6−√2)cmDnone of theseTwo sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be
A3.6 cmB4.1 cmC3.8 cm.D3.4 cm
Find the length of the third side of the triangle.
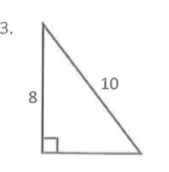
View SolutionFind the length of the third side of the triangle.
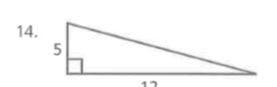
View SolutionTwo sides of a triangle are 2√2and2√3cm and the angle opposite to the shorter side of the two is π4. The largest possible length of the third side is
View SolutionIf length of two sides of a triangle are 6 cm and 10 cm, then the length of the third side can be
View SolutionThe lengths of the sides of a triangle are integral. If the perimeter of the triangle is 6cm, then how many such triangles are possible
View Solution
