Image of one the other line mirror To find the image of $L_{1} = 0$ through $L_{1} = 0$ first we find the point of intersection of $L_{1} = 0 and L_{1} = 0 .$ Let this is B. Again we take a point A on the line $L_{2}$ and find its image through $L_{1} = 0,$ let this is K.

Video Solution

Answer

Step by step video & image solution for Image of one the other line mirror To find the image of L_1=0 through L_1=0 first we find the point of intersection of L_1=0 and L_1=0. Let this is B. Again we take a point A on the line L_2 and find its image through L_1=0, let this is K. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS QUESTION BANK

Knowledge Check

Question 1 - Select One
Let $(2, - 1)$ be the point P and $x - y + 1 = 0$ be the straight line l. If $Q$ is image of point P about line, that image of point Q about y-axis is
A $(- 2, 3)$
B(2,3)
C(3,4)
D(-3,4)

If (-2,6) is the image of the point (4,2) with respect to line L=0, then L is:
View Solution
Find the distance of the point $P$ from the line $l$ in that : $l : 12 x - 7 = 0, P \equiv (3, - 1)$
View Solution
Find the distance of the point $P$ from the line $l$ in that : $l : 12 x - 7 = 0 \equiv (3, - 1)$
View Solution
Let S' be the image or reflection of the curve S = 0 about line mirror L = 0 Suppose P be any point on the curve S = 0 and Q be the image or reflection about the line mirror L = 0 then Q will lie on S' = 0
How to find the image or reflection of a curve ?

Let the given be S : f( x,y) = 0 and the line mirror L : $a x + b y + c = 0$ We take point P on the given curve in parametric form . Suppose Q be the image or reflection of point P about line mirror L = 0 which again contains the same parameter L et Q $\equiv (ϕ (t), (t)),$ where t is parameter . Now let $x = ϕ (t) and y = (t)$
Eliminating t , we get the equation of the reflected curve S'
The image of the circle $x^{2} + y^{2} = 4$ in the line $x + y = 2$ is
View Solution
Let S' be the image or reflection of the curve S = 0 about line mirror L = 0 Suppose P be any point on the curve S = 0 and Q be the image or reflection about the line mirror L = 0 then Q will lie on S' = 0
How to find the image or reflection of a curve ?

Let the given be S : f( x,y) = 0 and the line mirror L : $a x + b y + c = 0$ We take point P on the given curve in parametric form . Suppose Q be the image or reflection of point P about line mirror L = 0 which again contains the same parameter L et Q $\equiv (ϕ (t), (t)),$ where t is parameter . Now let $x = ϕ (t) and y = (t)$
Eliminating t , we get the equation of the reflected curve S'
The image of the parabola $x^{2} = 4 y$ in the line $x + y = a$ is
View Solution
The point C is the image of point A in line l and line segment BC intersects the line l at P.

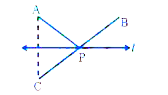
Is the image of P in line l the point P itself ?
View Solution
Let $(2, - 1)$ be the point P and $x - y + 1 = 0$ be the straight line l. If $Q$ is image of point P about line, that image of point Q about y-axis is
View Solution

Image of one the other line mirror To find the image of $L_{1} = 0$ through $L_{1} = 0$ first we find the point of intersection of $L_{1} = 0 and L_{1} = 0 .$ Let this is B. Again we take a point A on the line $L_{2}$ and find its image through $L_{1} = 0,$ let this is K.

Similar Questions

Knowledge Check

Let $(2, - 1)$ be the point P and $x - y + 1 = 0$ be the straight line l. If $Q$ is image of point P about line, that image of point Q about y-axis is

Recommended Questions

Image of one the other line mirror To find the image of L1=0 through L1=0 first we find the point of intersection of L1=0andL1=0. Let this is B. Again we take a point A on the line L2 and find its image through L1=0, let this is K.

Similar Questions

Knowledge Check

Let (2,−1) be the point P and x−y+1=0 be the straight line l. If Q is image of point P about line, that image of point Q about y-axis is

Recommended Questions

Image of one the other line mirror To find the image of $L_{1} = 0$ through $L_{1} = 0$ first we find the point of intersection of $L_{1} = 0 and L_{1} = 0 .$ Let this is B. Again we take a point A on the line $L_{2}$ and find its image through $L_{1} = 0,$ let this is K.

Let $(2, - 1)$ be the point P and $x - y + 1 = 0$ be the straight line l. If $Q$ is image of point P about line, that image of point Q about y-axis is