Lines L1=ax+by+c=0andL2=lx+my+n=0 intersect at the point P and make an anlge θ with each other. Find the equation of a line different from L2 with pass through P and makes the same anlge θ with L1.
The correct Answer is:2(al+bm)(ax+by+c)−(ax+by+c)−(a2+b2)(Ix+my+n)=0
Topper's Solved these Questions
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - SOLVED PROBLEMS (OBJECTIVE)
31 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - Exercise 1
3 Videos
- STRAIGHT LINE BOOK - FIITJEECHAPTER - STRAIGHT LINE EXERCISE - NUMERICAL BASED
4 Videos
- STATISTICSBOOK - FIITJEECHAPTER - STATISTICSEXERCISE - Comprehension Type
6 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
328 Videos
Similar Questions
Lines L1≡ax+by+c=0 and L2≡lx+my+n=0 intersect at the point P and make an angle θ with each other. Find the equation of a line different from L2 which passes through P and makes the same angle θ with L1.
View Solutionlines L1:ax+by+c=0 and L2:lx+my+n=0 intersect at the point P and make a angle θ between each other. find the equation of a line Ldifferent from L2 which passes through P and makes the same angle θ with L1
View Solution
Knowledge Check
Find the equation of the line which passes through the point (3,-4) and makes an anlge of 60∘ with the positive direction of x-axis :
Ax√2+y√3=0B√3x−y=4+3√3Cx√3+y=3√2+5Dnone of (a) , (b) ,(c)If l, m, n are in AP, then the line lx+my+n=0 will always pass through the point
A(-1, 2)B(1, -2)C(1, 2)D(2, 1)
lines L1:ax+by+c=0 and L2:lx+my+n=0 intersect at the point P and make a angle θ between each other. find the equation of a line Ldifferent from L2 which passes through P and makes the same angle θ with L1
View SolutionLines L1≡ax+by+c=0 and L2≡lx+my+n=0 intersect at the point P and make an angle θ with each other. Find the equation of a line different from L2 which passes through P and makes the same angle θ with L1.
View SolutionTwo lines l and m interset at the O and P is Point on a line n Passing through the point O such that P is equidistant from l and m. Prove that n is the bisectof the angle formed by l and m
View SolutionTwo lines l and m interset at the O and P is Point on a line n Passing through the point O such that P is equidistant from l and m. Prove that n is the bisectof the angle formed by l and m
View Solutionif line 2x+7y−1=0 intersect the lines L1:3x+4y+1=0andL2:6x+8y−3=0 in AandB respectively, then equation of line parallal to L1andL2 and passes through a point P such that AP:PB=2:1 (internally) is (P is on the line 2x+7y−1=0)
View SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
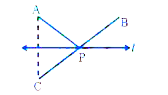
Is the image of P in line l the point P itself ?
View Solution
