In a △OAB, E is the mid-point of BO and D is a point on AB such that AD : DB = 2:1. If OD and AE intersect at P, determine the ratio OP: PD using vector method.
The correct Answer is:3:2
Step by step video, text & image solution for In a triangleOAB, E is the mid-point of BO and D is a point on AB such that AD : DB = 2:1. If OD and AE intersect at P, determine the ratio OP: PD using vector method. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In a △OAB,E is the mid point of OB and D is the point on AB such that AD:DB=2:1 If OD and AE intersect at P then determine the ratio of OP:PD using vector methods
View SolutionIn ΔABC,D is point on side AB and E is a point on side AC such that ∠ADE=∠ABC,AD=2,BD=3 and AE=3, then what is the value of CE ?
View Solution
Knowledge Check
In a triangle OAB, E is the midpoint of OB and D is a point on AB such that AD:DB=2:1. IF OD and AE intersects at P, then ratio of OPPD is equal to
A3:2B2:3C3:4D4:3In a ΔABC,D is the mid - point of BC and E is mid - point of AD, BF passes through E. What is the ratio of AF:FC?
 A1:1B1:2C1:3D2:3
A1:1B1:2C1:3D2:3D,E,F are the mid points of BC,CAandAB of ΔABC. If ADandBE intersect in G, then AG+BG+CG is equal to
AAD=BE=CFB23(AD+BE+CF)C32(AD+BE+CF)D13(AD+BE+CF)
In the given figure, in △ABC, D is the mid-point cf AB and P is any point on BC. If CQ∣∣PD meets AB in Q and area of △ABC=30cm2, then, area of △BPQ is
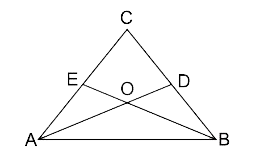
View SolutionIn the given figure ∠ABC=∠BAC , D and E are pointts on BC and AC respectively such that DB = AE . If AD and BE intersect at O then prove that OA = OB
View SolutionIn a triangle PQR,SandT are points on QRandPR, respectively, such that QS=3SRandPT=4TR. Let M be the point of intersection of PSandQT. Determine the ratio QM:MT using the vector method .
View SolutionIn a triangle ABC,DandE are points on BCandAC, respectivley, such that BD=2DCandAE=3EC. Let P be the point of intersection of ADandBE. Find BP/PE using the vector method.
View SolutionFor a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
View Solution