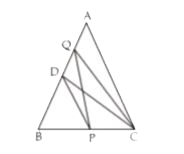
In the given figure, in △ABC, D is the mid-point cf AB and P is any point on BC. If CQ∣∣PD meets AB in Q and area of △ABC=30cm2, then, area of △BPQ is
Step by step video & image solution for In the given figure, in triangle ABC, D is the mid-point cf AB and P is any point on BC. If CQ || PD meets AB in Q and area of triangle ABC = 30 cm2, then, area of triangle BPQ is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
In triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2× area (ΔBPQ)= area (ΔABC)
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

View Solution
Knowledge Check
The triangle is formed by joining the mid-points of the sides AB,BC and CA of △ABCand the area of △PQR is 6cm2, then the area of △ABC is :
A36cm2B12cm2C18cm2D24cm2In triangle ABC, AD, BE and CF are the medians intersecting at point G and area of triangle ABC is 156cm2. What is the area (in cm2) of triangle FGE ?
A13B26C39D52
In Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC

View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC

View SolutionIn the given figure ABC is a triangle. D is mid point of AB. Q is a point of AB and P is a point of BC. DP||QC 1. Find out of relation between ΔABC&ΔQBP.
View SolutionIn a triangle ABC,∠B=90∘,D is the midpoint of AC,BD=√117. Sum of sides of AB & BC is 30 cm. Find the area of triangle ABC.
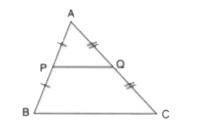
View SolutionIn triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 , find the perimeter of the trapezium PBCQ.
View Solution
