A resistance R of thermal coefficient of resistivity $α$ is connected in parallel with a resistance 3R having thermal coefficient of resistivity $2 α$ . Find the value of $α_{e f f}$

Video Solution

Text Solution

Verified by Experts

$α_{eff} = \frac{5}{4} α$ .

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

BOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 (Level -II) SECTION C,D - Circuit theory , KCL & KVL , Battery , Grouping of cells
9videos
CURRENT ELECTRICITY
BOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 (Level -II) SECTION E- Electrical Power & Energy
3videos
CURRENT ELECTRICITY
BOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 (Level -II) SECTION A- Definition of Current , Current Density , Drift Velocity
1videos
CURRENT ELECTRICITY
BOOK - MOTIONCHAPTER - CONSTRAINED MOTION EXERCISE - EXAMPLES
12videos
CONSTRAINED MOTION
BOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -3
60videos
ELASTICITY

Similar Questions

Knowledge Check

Question 1 - Select One
A wire of cross-section area $A$ , length $L_{1}$ , resistivity $ρ_{1}$ and temperature coefficient of resistivity $α_{1}$ is connected in series to a second wire of length $L_{2}$ , resistivity $ρ_{2}$ temperature coefficient of resistivity $α_{2}$ and the same area $A$ , so that wires carry same current. Total resistance $R$ is independent of temperature for small temperature change if (Thermal expansion effect is negligible)
A $α_{1} = - α_{2}$
B $ρ_{1} L_{1} α_{1} + ρ_{2} L_{2} α_{2} = 0$
C $L_{1} α_{1} + L_{2} α_{2} = 0$
DNone
Question 2 - Select One
If a resistance $R_{2}$ is connected in parallel with the resistance $R$ in the circuit shown, then possible value of current through $R$ and the possible value of $R_{2}$ will be

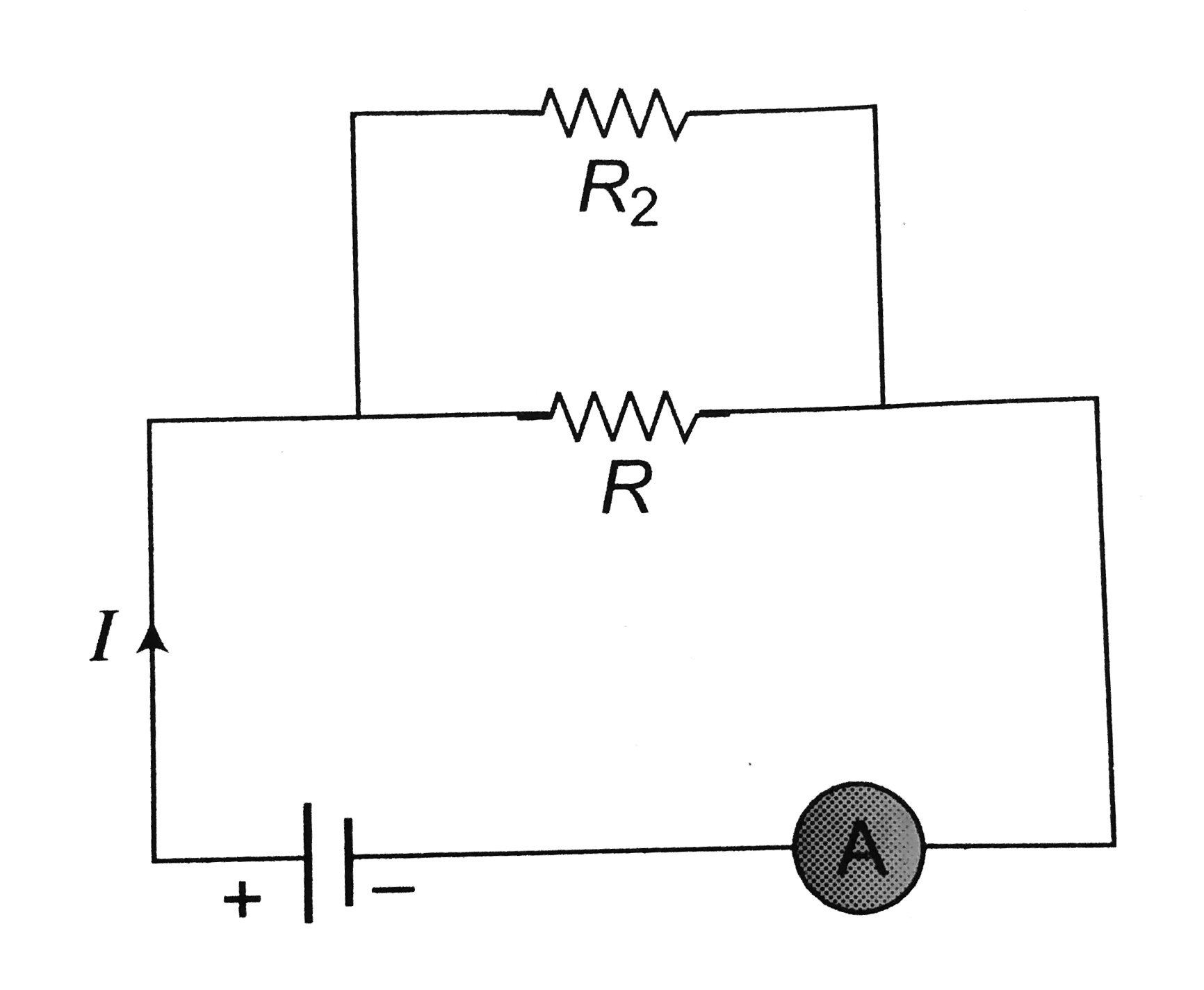A $\frac{I}{3}, R$
B $I .2 R$
C $\frac{I}{3}, 2 R$
D $\frac{I}{2}, R$
Question 3 - Select One
Two equal resistance at $0^{\circ} C$ with temperature coefficient of resistance $α_{1}$ and $α_{2}$ joined in series act as a single resistance in a circuit the temperature coefficient of their single resistance will be
A $α_{1} + α_{2}$
B $\frac{α_{1} α_{2}}{α_{1} + α_{2}}$
C $\frac{α_{1} - α_{2}}{2}$
D $\frac{α_{1} + α_{2}}{2}$

MOTION-CURRENT ELECTRICITY-EXERCISE -3 (Level -II) SECTION B- Resistance & resistivity ,Ohms law +VI (Volt - Curr.) Characteristics + Colour Code + Temp . Dependence

Home
Ask Doubt
Profile