The acceleration down the plane of spherical body of mass m radius R and moment of inertia I having inclination θ to the horizontal is
gsinθ1+12/R2
gsinθ1+I/R2
gsinθ1+I/MR2
gsinθMR2+1
The correct Answer is:C
To solve the problem of finding the acceleration down the plane of a spherical body with mass m, radius R, and moment of inertia I inclined at an angle θ to the horizontal, we can follow these steps:
Step 1: Identify the Forces Acting on the Body
The forces acting on the spherical body include:
- The gravitational force mg acting downward.
- The component of gravitational force acting down the incline, which is mgsin(θ).
- The frictional force fs acting up the incline.
Step 2: Apply Newton's Second Law for Linear Motion
According to Newton's second law, the net force acting on the body along the incline can be expressed as:
mgsin(θ)−fs=ma
where a is the acceleration of the center of mass of the spherical body.
Step 3: Apply the Torque Equation
Next, we consider the rotational motion about the center of mass. The torque τ due to the frictional force is given by:
τ=fs⋅R
This torque is also related to the angular acceleration α of the body:
τ=Iα
Since the linear acceleration a is related to angular acceleration by the equation a=Rα, we can substitute α as aR:
fs⋅R=I(aR)
From this, we can express the frictional force:
fs=IaR2
Step 4: Substitute the Frictional Force Back into the Linear Motion Equation
Now, we substitute the expression for fs back into the linear motion equation:
mgsin(θ)−IaR2=ma
Step 5: Rearrange the Equation to Solve for Acceleration a
Rearranging the equation gives:
mgsin(θ)=ma+IaR2
Factoring out a from the right side:
mgsin(θ)=a(m+IR2)
Now, we can solve for a:
a=mgsin(θ)m+IR2
Final Result
Thus, the acceleration down the plane of the spherical body is:
a=gsin(θ)1+ImR2
The forces acting on the spherical body include:
- The gravitational force mg acting downward.
- The component of gravitational force acting down the incline, which is mgsin(θ).
- The frictional force fs acting up the incline.
According to Newton's second law, the net force acting on the body along the incline can be expressed as:
mgsin(θ)−fs=ma
where a is the acceleration of the center of mass of the spherical body.
Next, we consider the rotational motion about the center of mass. The torque τ due to the frictional force is given by:
τ=fs⋅R
This torque is also related to the angular acceleration α of the body:
τ=Iα
Since the linear acceleration a is related to angular acceleration by the equation a=Rα, we can substitute α as aR:
fs⋅R=I(aR)
From this, we can express the frictional force:
fs=IaR2
Now, we substitute the expression for fs back into the linear motion equation:
mgsin(θ)−IaR2=ma
Rearranging the equation gives:
mgsin(θ)=ma+IaR2
Factoring out a from the right side:
mgsin(θ)=a(m+IR2)
Now, we can solve for a:
a=mgsin(θ)m+IR2
Thus, the acceleration down the plane of the spherical body is:
a=gsin(θ)1+ImR2
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 240videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-A )46videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-B )24videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-438videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 334videos
SEMI CONDUCTOR AND LOGIC GATES
Similar Questions
Consider a system of a small body of mass m kept on a large body of mass M placed over an inclined plane of the angle of inclination θ to the horizontal. Find the acceleration of m when the system is set in motion. Assume an inclined plane to be fixed. all the contact surfaces are smooth.
 View Solution
View SolutionThe pulleys in filgure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
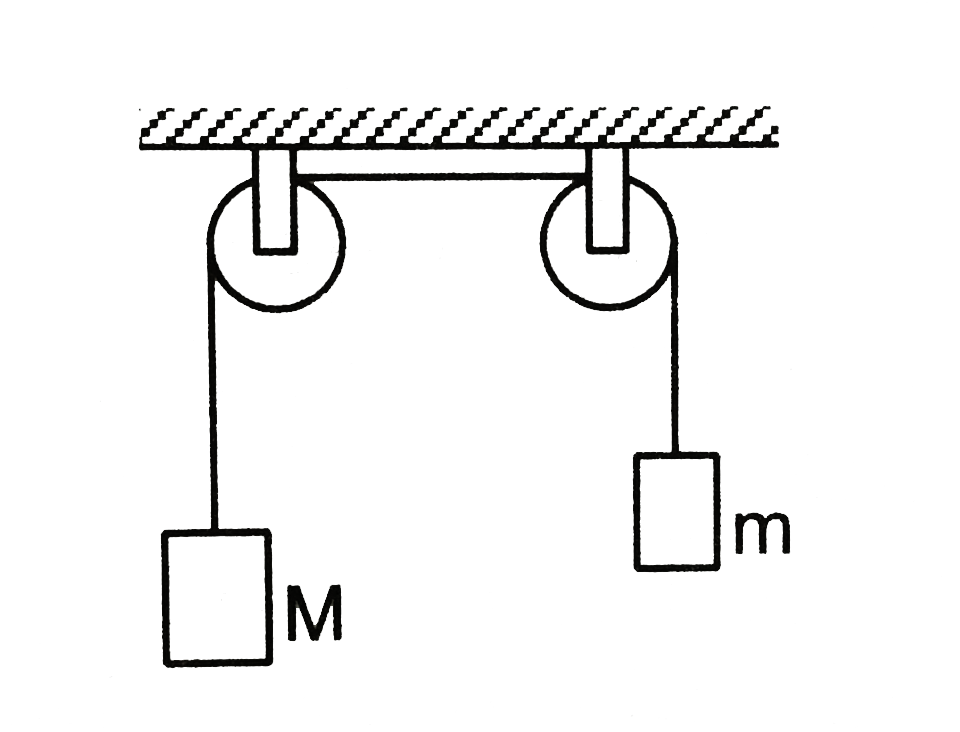 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
When a body is placed on a rough plane inclined at an angle θ to the horizontal, its acceleration is
Ag(sinθ−cosθ)Bg(sinθ−μcosθ)Cg(μsinθ1−cosθ)Dgμ(sinθ−cosθ) - Question 2 - Select One

A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k isA34MgsinθkB2MgsinθkCMgsinθkDnone of these - Question 3 - Select One
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
Find moment of inertia of a sector of mass M , radius R and of central angle θ radians .
View SolutionA cotton reel of mass m, radius R and moment of inertia I is kept on a smooth horizontal surface. If the string is pulled horizontally by a force F, find the (i) acceleration of CM, (ii) angular acceleration of the cotton reel.
 View Solution
View SolutionFind moment of inertia of a sector cut from a disc of mass M, radius R and central angle θ
View SolutionA round unifrom body of radius R, mass M and moment of inertia I rolls down (without slipping) an inclined plane making an angle theta with the horizontal. Then its acceleration
View SolutionThe ratio of the accelerations for a solid sphere (mass m,andradiusR) rolling down an incline of angle θ without slipping, and slipping down the incline without rolling is
View Solution

