Consider a system of a small body of mass m kept on a large body of mass M placed over an inclined plane of the angle of inclination θ to the horizontal. Find the acceleration of m when the system is set in motion. Assume an inclined plane to be fixed. all the contact surfaces are smooth.

Method 1: Analysis in an inertial reference frame attached to the ground :
Let a be the acceleration m w.r.t. M directed horizontally towards right.
Let A be the acceleration of M w.r.t. the ground directed along the incline downwards.

Acceleration of m w.r.t. ground will be the vector sum of the acceleration of m w.r.t. M and the acceleration of M w.r.t. ground.
force equation for m are
0=m(a−Acosθ) ..(i)
mg−N'=m(Asinθ) ...(ii)
Force equation for M are
N'sinθ+Mgsinθ=MA ...(iii)
N'cosθ+Mgcosθ−N=0 ...(iv)
from (ii),
N'=mg−mAsinθ
Subsitituting N' in (iii),
(mg−mAsinθ)sinθ+Mgsinθ=MA
⇒A=(M+m)gsinθM+msin2θ
Acceleration of m w.r.t. ground is Asinθ (since, Acosθ−a=0). Thus, the acceleration of m w.r.t. ground is
amG=Asinθ=(M+m)gsinθM+msin2θ
Method 2: Analysis of motion of m in the non-inertial reference frame attached to M:
Let the acceleration of M w.r.t ground be A along the inclined plane downwards. Consider that ground is an inertiail reference frame, the reference frame attached to M will be non-inertial . For applying Newton's second law of motion to any object w.r.t. on the object which equals mass of the objects times accelerations of M, directed opposite to A.
Force equation for m:
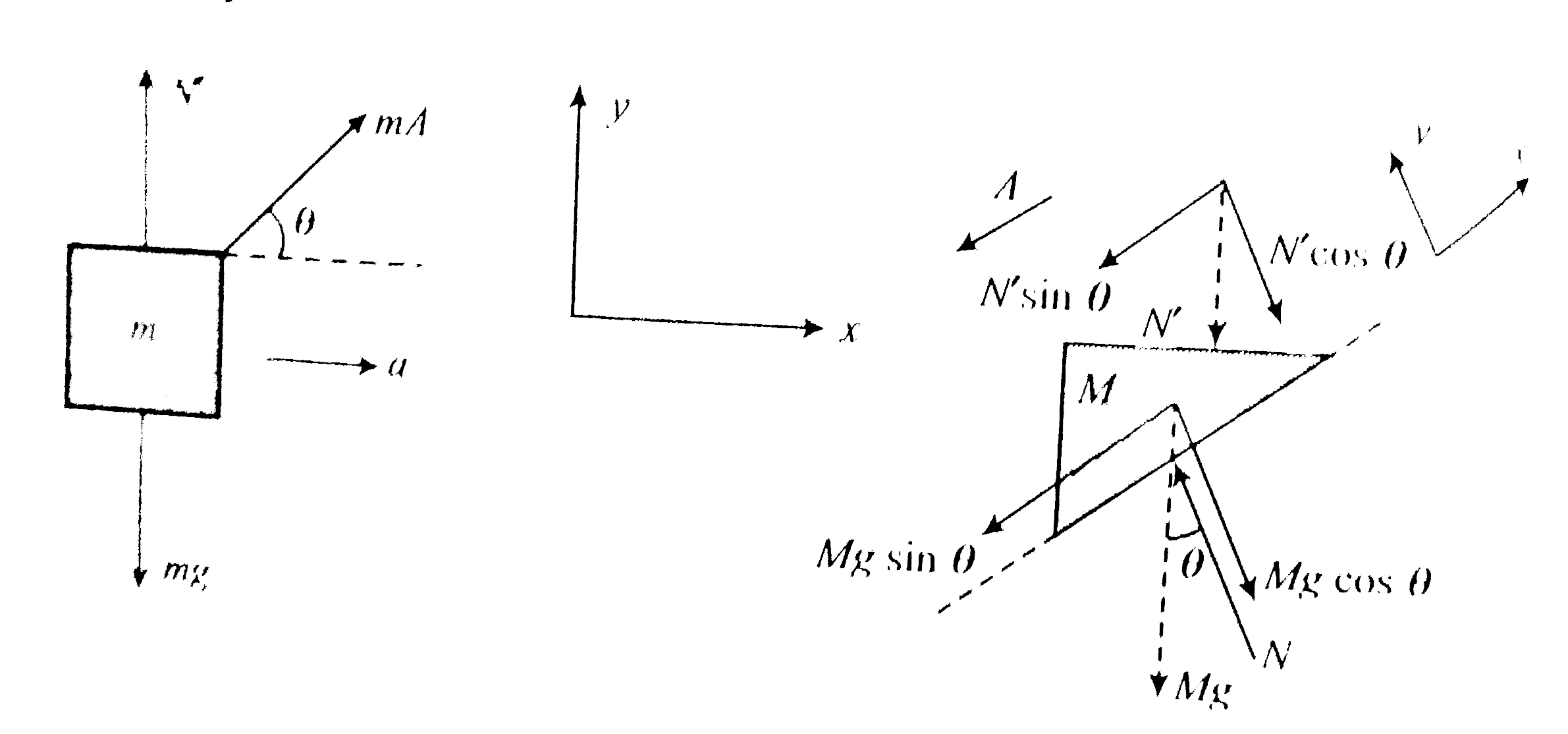
Let the acceleration of m w.r.t. M be a, in the horizontal direction towards right.
The force acting on m are:
∗weight of m, mg, acting vertically downwards
∗ Normal force on m by M, N' , vertically upwards, and
∗ (mA), the inertial force acting along the incline upwards, as the acceleration of M is A along the incline downwards.
N'+(mA)sinθ=mg ..(i)
(mA)cosθ=ma ..(ii)
Force equation for M:
The force acting on M are
∗ The weight Mg
∗N', normal force exerted by m
∗N, normal force exerted by the incline
Mgsinθ+N'sinθ=MA..(iii)
(Along the incline)
Mgcosθ+N'cosθ=N ...(iv)
(Perpendicular to the incline)
From (i),(iii) and (iv)
A=(M+m)gsinθM+msin2θ
Acceleration of m relative to ground.
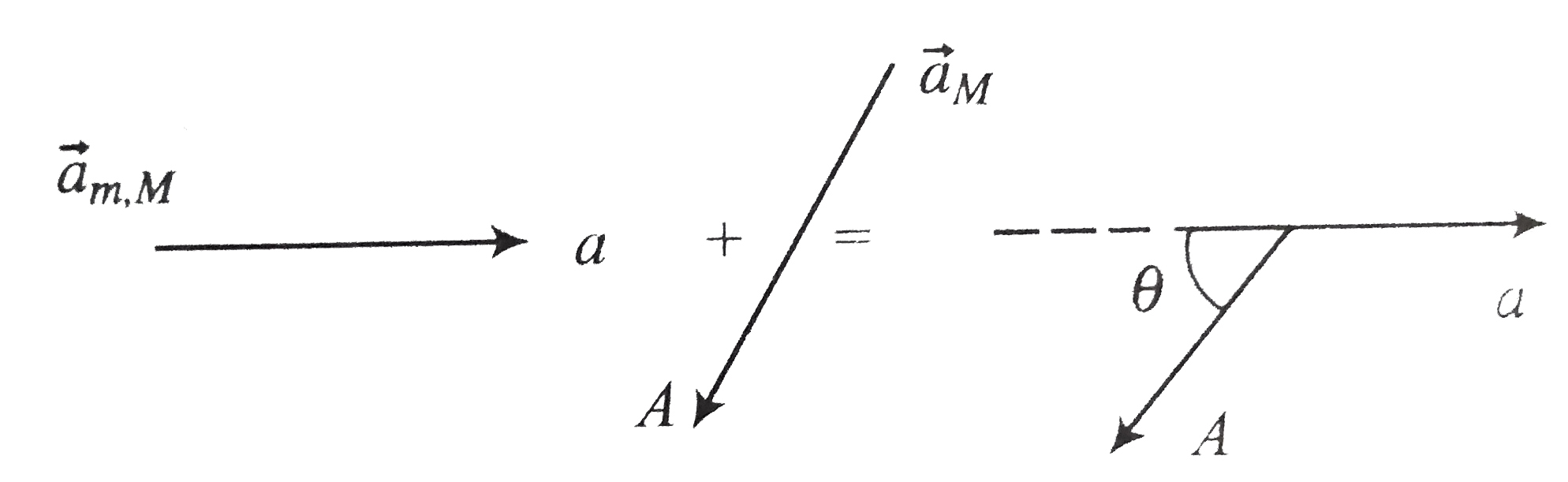
→am=→amM+→aM
=aˆi+Acosθ(−ˆi)+Asinθ(−ˆj)
But a=Acosθ [ form(ii)], therefore,
am=Asinθ, vertically downward
(M+m)gsin2θM+msin2θ
Method 3: Considering M and m as system

The system has (M+m)gsinθ external force parallel to inclined plane.
→Fx'=M(→aM)x'+m(→am)x'
(→am)x'=(→am,M)x'+(→aM)x'
=−acosθ+A=(A−acosθ)
MA+m(A−acosθ)=(M+m)gsinθ ...(i)
Considering the motion of block in horizontal direction only and writing equation of motion w.r.t. ground,
(→am)x=a−Acosθ
The block is not having any external force in horizontal direction
Σ→Fx=0=m(→am)x=m(a=Acosθ)
or a=Acosθ ...(ii)
From (i) and (ii)
MA+m[A−(Acosθ)cosθ]=(M+m)gsinθ
MA+mAsin2θ=(M+m)gsinθ
After solving, we get
A=(M+m)gsinθM+msin2θ
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A rigid body of mass m and radius r starts coming down an inclined plane of inclination θ . Then find out the acceleration of centre of mass if friciton is absent.
View SolutionA block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View Solution
Knowledge Check
When a body is placed on a rough plane inclined at an angle θ to the horizontal, its acceleration is
Ag(sinθ−cosθ)Bg(sinθ−μcosθ)Cg(μsinθ1−cosθ)Dgμ(sinθ−cosθ)A body is freely rolling down on an inclined plane whose angle of inclination is θ. If a is acceleration of its centre of mass then following is correct
Aa=gsinθBa<gsinθCa>gsinθDa=0A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
A75gsinθB27gsinθC37gsinθD57gsinθ
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA body of mass m is kept on a rough fixed inclined plane of angle of inclination θ=30∘. It remains stationary. Then magnitude of force acting on the body by the inclined plane is equal to :
View SolutionA body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
View Solution
