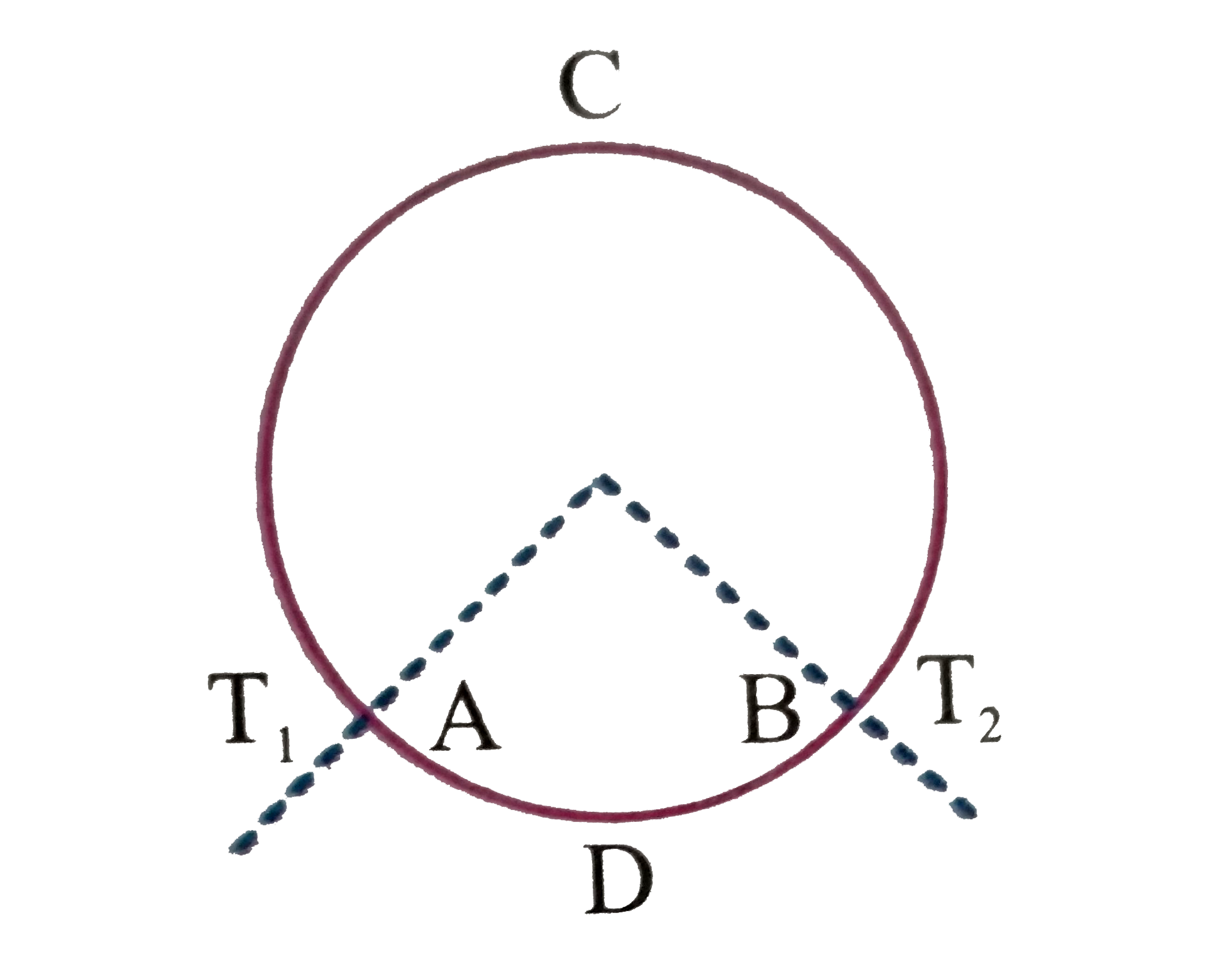
A ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H The ADB part is now replaced with another metal keeping the temperature T91) and T2 constant The heat carried increases to 2H What should be the conductivity of the new ADB Given ACBADB=3
 .
.
73k
2k
52k
3k
The correct Answer is:A
Step by step video & image solution for A ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H The ADB part is now replaced with another metal keeping the temperature T_91) and T_(2) constant The heat carried increases to 2H What should be the conductivity of the new ADB Given (ACB)/(ADB)=3 . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEAT TRANSFER & THERMAL EXPANSION BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - Exercise - 3 Section-A
21 Videos
- HEAT TRANSFER & THERMAL EXPANSION BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - Exercise - 3 Section-B
19 Videos
- HEAT TRANSFER & THERMAL EXPANSION BOOK - MOTIONCHAPTER - HEAT TRANSFER & THERMAL EXPANSION EXERCISE - EXERCISE - 1
60 Videos
- HEAT - 1BOOK - MOTIONCHAPTER - HEAT - 1EXERCISE - EXERCISE -4 (Level - II) Previous Year | JEE Advanced
22 Videos
- HEAT-2 BOOK - MOTIONCHAPTER - HEAT-2 EXERCISE - EXERCISE-4 (LEVEL-II)
30 Videos
Similar Questions
A ring consisting of two parts ADB and ACB. of same conductivity K carries an amount of heat H. The ADB part is now replaced with another metal keeping the temperature T1 and T2 constant. The heat carried increases to 2H. The conductivity of the new ADB part is x3K. Find the value of x, (Given: ACBADB=3 ) .
'(##CEN_KSR_PHY_JEE_C13_E01_003_Q02##)'
View SolutionA rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k=a/T, where a is a constant. The ends of the rod are kept at temperatures T1andT2. Find the function T(x), where x is the distance from the end whose temperature is T1.
View Solution
Knowledge Check
Consider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
AK1A1=K2A2BK2A1=K1A2CK1A1S1=K2A2S2DK2A1S2=K1A2S1A rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
AAαT21−T22lBAαT21+T22lCAαT21+T223lDAαT21−T222lA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
AAα(T21−T22)lBAα(T21+T22)lCAα(T21+T22)3lDAα(T21−T22)2l
A window with double-pane is used for insulating a room thermally from outside. It consists of two glass sheets, each of area A and thickness d with a separation x between them. At equilibrium, the room-glass interface and glass-outside interface are at constant temperature of Tr and Ta respectively. What will the rate of heat flow through the window pane? The thermal conductivity of glass and air are K1 and K2 , respectively.
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
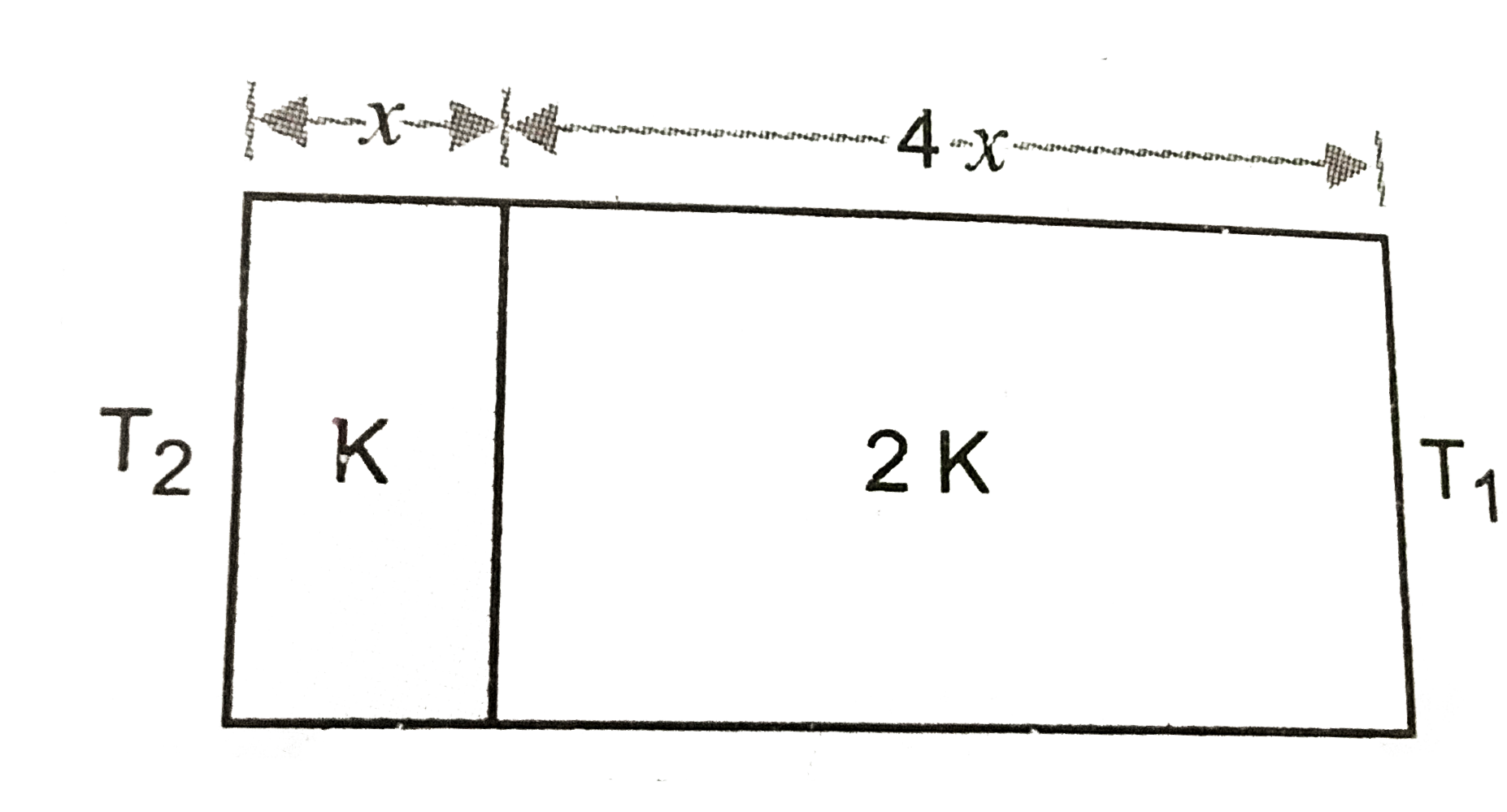
View SolutionA composite slab consists of two rectangular slabs of different materials, having coefficients of conductivity 2K and K. The two ends of the slabs are at temperatures T1 and T2 (where T1>T2 ). How will the rate of heat flow depend on a where 3a and a are the lengths of two slabs? Consider that the two slabs have equal thickness.

View SolutionTwo rods A and B have lengths l1andl2. Each rod has its ends at temperature T1andT2 Radii fo cross section of the two rods are same. The condition for equal flow of heat through those two rods is (K1,K2 are thermal conductivities of two rods)
View Solution
