Let A(0,0),B(3,0),C(2,1) then area of the square inscribed in the triangle such that,one side of the square is taken along ¯¯¯¯¯¯AB
Step by step video & image solution for Let A(0,0), B(3,0), C (2, 1) then area of the square inscribed in the triangle such that,one side of the square is taken along bar(AB) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A circle is inscribed in an equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is______
View SolutionA circle is inscribed in an equilateral triangle of side a, The area of the square inscribed in the circle,in sq.units is
View SolutionIF twice the square of the radius of a circle is equal to half the sum of the squares of the sides of inscribed triangle ABC, then sin2A+sin2B+sin2C=
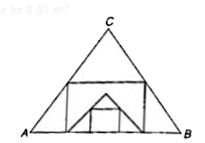
View SolutionIn the adjoining figure ABC is an equilateral triangle inscribeing a square of maximum possible area . Again in this square there is an equilateral triangle whose side is same as that of the square . Further the smaller equilateral triangle inscribes a square of maximum possible area . What is the area of the innermost square if the each side of the outermost triangle be 0.01 m ?
View SolutionFind the coordinates of the vertices of a square inscribed in the triangle with vertices A(0,0),B(3,0)andC(2,1); given that two of its vertices are on the side AB.
View SolutionA circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in this circle is
View SolutionFind the coordinates of the vertices of a square inscribed in the triangle with vertices A(0,0),B(3,0) a n d C(2,1); given that two of its vertices are on the side A Bdot
View SolutionFind the area of the triangle inscribed in a circle circumscribed by a square made by joining the midpoints of the adjacents sides of a square of side x?
View Solution
