Let AD be a median of the ABC. If AEandAF are medians of the triangle ABDandADC , respectively, and AD=m1,AE=m2,AF=m3, thena28 is equal to (a)m22+m23−2m21 (b) m21+m22−2m23 (c)m21+m23−2m22 (d) none of these
Step by step video & image solution for Let A D be a median of the A B Cdot If A Ea n dA F are medians of the triangle A B Da n dA D C , respectively, and A D=m_1,A E=m_2,A F=m_3, then(a^2)/8 is equal to (a)m_2^2+m_3^2-2m_1^2 (b) m_1^2+m_2^2-2m_3^2 (c)m_1^2+m_3^2-2m_2^2 (d) none of these by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
In a ABC, D, E, F are the mi-points of sides BC, CA and AB respectively. If ar(ABC)=16cm2, then ar (trapezium FBCE)= 4 cm2 (b) 8 cm2 (c) 12cm2 (d) 10cm2
View SolutionIf y+3=m1(x+2) and y+3=m2(x+2) are two tangents to the parabola y2=8x, then (a)m1+m2=0 (b) m1+m2=−1 (c)m1+m2=1 (d) none of these
View Solution
Knowledge Check
Let AD be a median of the ΔABC. If AE and AF are medians of the triangle ABD and ADC, respectively, and AD = m1,AE=m2,AF=m3, then a2/8 is equal to
Am22+m23−2m21Bm21+m22−2m23Cm21+m23−2m22Dnone of theseAD is a median of the ΔABC . If AE and AF are medians of the triangles ABD and ADC repectively , and AD=m1,AE=m2,AF=m3, then m22+m23−2m21=
Aa2Ba22Ca24Da28In triangle ABC m1,m2,m3 are the lenghts of the medians through A,B and C respectively . If C=π2, then m21+m22m23=
A2B3C4D5
In a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
View SolutionA line x+3y=12 cuts the xandy axis in AandB respectively. If PandQ being the points of trisection of AB(P being closer to A) and m1,m2 are the slope of the lines OP and OQ respectively ('O' is the origin), then m2=2m1 (b) m2=3m1 m2=4m1 (d) m2=5m1
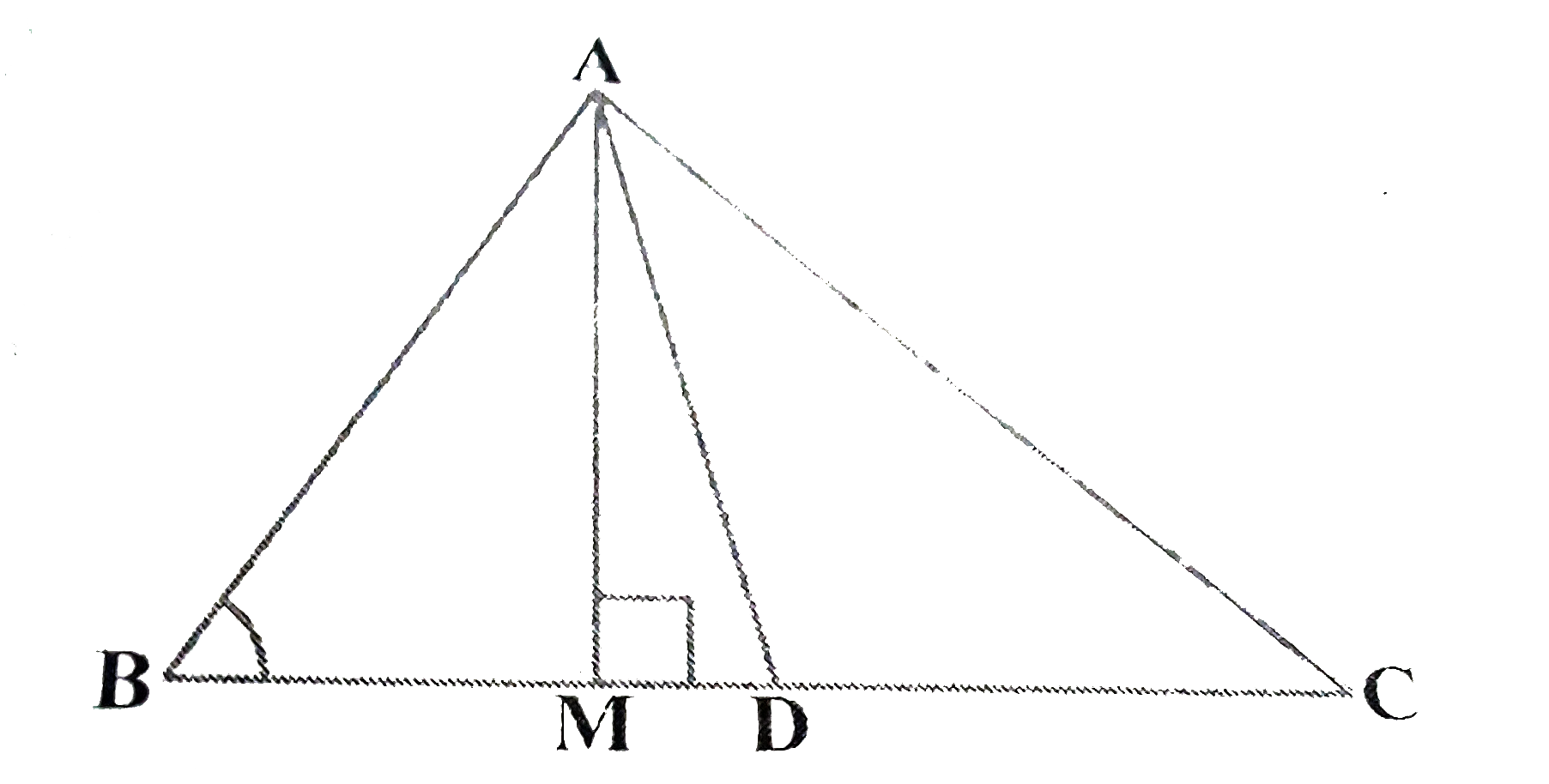
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View SolutionIf y=sin(m sin−1x) , then (1−x2)y2−xy1 is equal to m2y (b) my (c) −m2y (d) none of these
View SolutionIf 3m−13m=3,m≠0, then m2+181m2 is equal to
View Solution
