In a ABC, D, E, F are the mi-points of sides BC, CA and AB respectively. If ar(ABC)=16cm2, then ar (trapezium FBCE)= 4 cm2 (b) 8 cm2 (c) 12cm2 (d) 10cm2
Area (△ABC)=16cm2
Area(trap.FBCE)= △ABC−△AFE
14area(△ABC)=area(△AFE)
area(△AFE)=14×16=4cm2
NOW, area of trapezium=16−4=
12cm2
Hence, option (c) is correct.
Topper's Solved these Questions
Similar Questions
In a ABC if D and E are mid-points of BC and AD respectively such that ar (AEC)=4 cm2 , then ar (BEC)= 4 cm2 (b) 6 cm2 (c) 8 cm2 (d) 12cm2
View SolutionMedians of ABC intersect at G . If ar (ABC)=27 cm2, then ar (ABGC)= 6 cm2 (b) 9 cm2 (c) 12 cm2 (d) 18cm2
View SolutionIn Figure, ABCDandFECG are parallelograms equal in area. If ar(AQE)=12cm2, then ar(IIgm)FGBQ)=
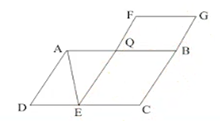
(a)12cm2
(b) 20cm2
(c) 24cm2
(d) 36cm2View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionABCDEF . If BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)= 108cm2 (b) 96cm2 (c) 48cm2 (d) 100cm2
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)View SolutionA, B, C, D are mid-points of sides of a parallelogram PQRS. If ar (PQRS)=36cm2, then ar(ABCD)= 24 cm2 (b) 18 cm2 (c) 30 cm2 (d) 36 cm2
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LCM)=ar(LBM)View Solution

