For a particle in uniform circular motion the acceleration →a at a point P(R,θ) on the circle of radius R is : ( here θ is measured from the x- axis )
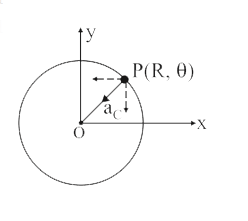
A
−v2Rcosθˆi+v2Rsinθˆj
B
−v2Rsinθˆi+v2Rcosθˆj
C
−v2Rcosθhai−v2Rsinθˆj
D
v2Rˆi+v2Rˆj
Video Solution
Text Solution
The correct Answer is:D
For a particle in uniform circular motion, acceleration a=v2R is toward the centre. From figure, we have −a=−acosθˆi−asinθˆj⇒−a=−v2Rcosθˆi−v2Rsinθˆj
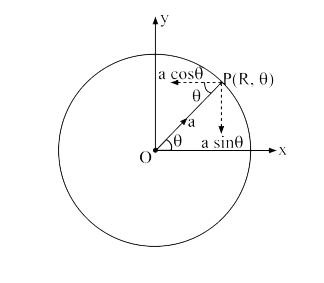
|
Similar Questions
Knowledge Check
For a particle performing a uniform circular motion the acceleration is
Aconstant in directionBconstant in magnitude but not in directionCconstant in magnitude and directionDconstant neither in magnitude nor in direction.For a particle in uniform circular motion , the acceleration →a at a point p(R,θ) on the circle of radiu R is ( Here θ is measured from the x−aξs )
A−v2Rcosθˆi+v2RsinθˆjB−v2Rsinθˆi+v2RcosθˆjC−v2Rcosθˆi−v2RsinθˆjD−v2Rˆi+v2RˆjIn a non uniform circular motion, the acceleration on the particle is
Acentripetal acceleration onlyBtangential acceleration onlyCthe resultant centripetal and tangential accelerationDcentrifugal acceleration
For a particle in a non-uniform accelerated circular motion
View SolutionThe area of a sector of angle θ∘ of a circle with radius R is
View SolutionA particle is moving an a uniform circular motion with radius 'r' Then the distance covered by the particle on one revoution will be
View SolutionThe force acts ona particle perfoming uniform circular motion and which is directed towards centre along radius of circle is
View SolutionThe length of an arc of a sector of angle θ∘ of a circle with radius R is
View Solution
