A particle placed
1.inside a uniform spherical shell of mass M, but not at the center
2.inside a uniform spherical shell of mass M, at the center
3.outside a uniform spherical shell of mass M, a distance r from the center
4.outside a uniform solid sphere of mass M, a distance 2r from the center
If F1,F2,F3 and F4 are gravitational forces acting on the particle in four cases.
F1>F2>F3>F4
F1=F2<F3<F4
F1=F2<F4<F3
F1<F2<F3<F4
The correct Answer is:C
To solve the problem, we will analyze the gravitational forces acting on a particle placed in four different scenarios involving a uniform spherical shell and a solid sphere. We will denote the gravitational forces in each case as F1,F2,F3, and F4.
1. Case 1: Inside a Uniform Spherical Shell (Not at the Center)
- According to the Shell Theorem, the gravitational field inside a uniform spherical shell is zero at any point inside the shell.
- Therefore, the gravitational force F1 acting on the particle is:
F1=0
2. Case 2: Inside a Uniform Spherical Shell (At the Center)
- Similar to Case 1, since the particle is still inside the shell, the gravitational field remains zero at the center as well.
- Thus, the gravitational force F2 acting on the particle is:
F2=0
3. Case 3: Outside a Uniform Spherical Shell (Distance r from the Center)
- When the particle is outside the shell, we can treat the shell as a point mass located at its center. The gravitational force F3 can be calculated using Newton's law of gravitation:
F3=GMmr2
4. Case 4: Outside a Uniform Solid Sphere (Distance 2r from the Center)
- Similar to Case 3, for a solid sphere outside its surface, we can also treat it as a point mass at its center. The gravitational force F4 is given by:
F4=GMm(2r)2=GMm4r2
Summary of Forces:
- F1=0
- F2=0
- F3=GMmr2
- F4=GMm4r2
Comparison of Forces:
- Since F1=0 and F2=0, we have:
F1=F2<F4<F3
- This means:
0<GMm4r2<GMmr2
Final Conclusion:
The correct order of the gravitational forces is:
F1=F2<F4<F3
- According to the Shell Theorem, the gravitational field inside a uniform spherical shell is zero at any point inside the shell.
- Therefore, the gravitational force F1 acting on the particle is:
F1=0
- Similar to Case 1, since the particle is still inside the shell, the gravitational field remains zero at the center as well.
- Thus, the gravitational force F2 acting on the particle is:
F2=0
- When the particle is outside the shell, we can treat the shell as a point mass located at its center. The gravitational force F3 can be calculated using Newton's law of gravitation:
F3=GMmr2
- Similar to Case 3, for a solid sphere outside its surface, we can also treat it as a point mass at its center. The gravitational force F4 is given by:
F4=GMm(2r)2=GMm4r2
- F1=0
- F2=0
- F3=GMmr2
- F4=GMm4r2
- Since F1=0 and F2=0, we have:
F1=F2<F4<F3
- This means:
0<GMm4r2<GMmr2
The correct order of the gravitational forces is:
F1=F2<F4<F3
Similar Questions
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass m is located outside a uniform sphere of mass M at a distance r from its centre. Find:
(a) the potential energy of gravitational interaction of the particle and the sphere,
(b) the gravitational force which the sphere exerts on the particle.View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
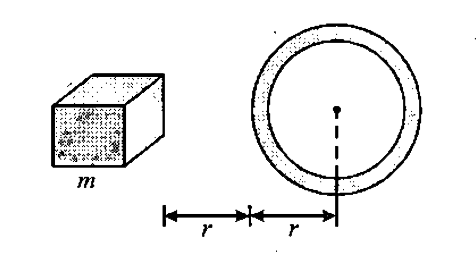 AOnly gravitational field inside the shell is zeroBGravitational field and gravitational potential both are zero inside the shellCGravitational potential as well as gravitational field inside the shell are not zeroDCan't be ascertained.
AOnly gravitational field inside the shell is zeroBGravitational field and gravitational potential both are zero inside the shellCGravitational potential as well as gravitational field inside the shell are not zeroDCan't be ascertained. - Question 2 - Select One
A particel of mass M is placed at the centre of a inform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
A−GMRB−3GMRC−2GMRDzero - Question 3 - Select One
A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
A−GmRB−3GmRC−4GmRD−2GmR
A particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionA : The gravitational field intensity is zero everywhere inside a uniform spherical shell
R: The net force on a point mass inside a uniform spherical shell is zero everywhere .View SolutionA particle of mass M is situated at the centre of a spherical shell of same mass and radius 'a'. The gravitational potential at a point situated at a2 distance from the centre, will be
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View Solution

