Two particles, each of mass m, are a distance d apart. To bring a third particle, also having mass m, from far away to the point midway between the two particles an external agent does work given by:
4Gm2/d
−4Gm2/d
4Gm2/d2
−4Gm2/d2
The correct Answer is:B
To solve the problem, we need to calculate the work done by an external agent to bring a third particle of mass m from far away to the midpoint between the two existing particles, each of mass m, which are separated by a distance d.
1. Identify the Position of the Third Particle:
The third particle is brought to the midpoint between the two particles. The distance from each of the two particles to the midpoint is d2.
2. Calculate the Gravitational Potential Energy:
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
In our case, we have two interactions to consider:
- The interaction between the third particle and the first particle.
- The interaction between the third particle and the second particle.
3. Potential Energy Between the Third Particle and Each of the Two Existing Particles:
- For the first particle:
U1=−Gmmd2=−2Gm2d
- For the second particle:
U2=−Gmmd2=−2Gm2d
4. Total Potential Energy When the Third Particle is at Midpoint:
The total potential energy Utotal when the third particle is at the midpoint is the sum of the potential energies from both interactions:
Utotal=U1+U2=−2Gm2d−2Gm2d=−4Gm2d
5. Work Done by the External Agent:
Since the third particle is brought from a point where the potential energy is zero (far away) to the midpoint, the work done W by the external agent is equal to the change in potential energy:
W=Utotal−Uinitial
Here, Uinitial=0 (at infinity):
W=−4Gm2d−0=−4Gm2d
Final Answer:
The work done by the external agent to bring the third particle to the midpoint is:
W=−4Gm2d
The third particle is brought to the midpoint between the two particles. The distance from each of the two particles to the midpoint is d2.
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
In our case, we have two interactions to consider:
- The interaction between the third particle and the first particle.
- The interaction between the third particle and the second particle.
- For the first particle:
U1=−Gmmd2=−2Gm2d
- For the second particle:
U2=−Gmmd2=−2Gm2d
The total potential energy Utotal when the third particle is at the midpoint is the sum of the potential energies from both interactions:
Utotal=U1+U2=−2Gm2d−2Gm2d=−4Gm2d
Since the third particle is brought from a point where the potential energy is zero (far away) to the midpoint, the work done W by the external agent is equal to the change in potential energy:
W=Utotal−Uinitial
Here, Uinitial=0 (at infinity):
W=−4Gm2d−0=−4Gm2d
The work done by the external agent to bring the third particle to the midpoint is:
W=−4Gm2d
Similar Questions
Two particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionTwo stationary particles of masses M1 and M2 are 'd' distance apart. A third particle lying on the line joining the particles, experiences no resultant gravitational force. What is the distance of this particle from M1 ?
View Solution
Knowledge Check
A particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
 AGravitational field and potential both are zero at centre of the shell.BGravitational field is zero not only inside the shell but at a point outside the shell also.CInside the shell, gravitational field alone is zeroDNeither gravitational field nor gravitational potential is zero inside the shell.
AGravitational field and potential both are zero at centre of the shell.BGravitational field is zero not only inside the shell but at a point outside the shell also.CInside the shell, gravitational field alone is zeroDNeither gravitational field nor gravitational potential is zero inside the shell.The reduce mass of two particles having masses m and 2 m is
A2 mB3 mC2 m/3Dm/2Two bodies of mass M and 4M kept at a distance y apart. Where should a small particle of mass m be placed from M so that the net gravitational force on it is zero
Ay5By2Cy4Dy3
Each of the four corners of a square with edge a is occupied by a point mass m. There is a fifth mass, also m, at the center of the square. To remove the mass from the center to a point far away the work that must be done by an external agent is given by:
View SolutionConsider a system of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass centre of particles at the original position?
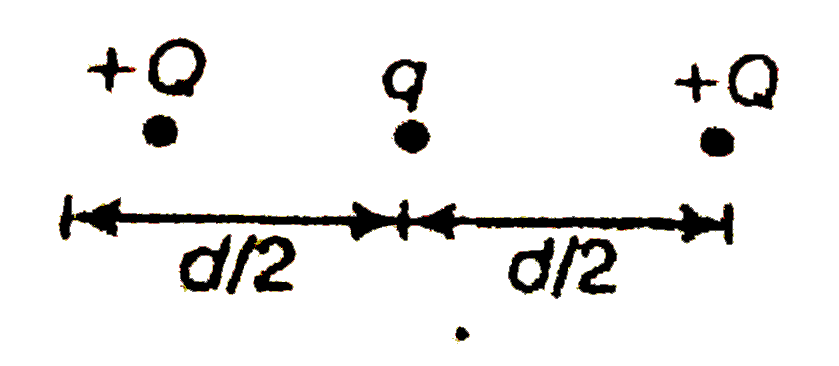
View SolutionTwo positively charged particles each having charge Q and are d distance apart. A third charge is introduced in midway on the line joining the two charges. Find the nature and magnitude of third charge so that the system is in equilibrium.
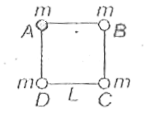
View SolutionFour particles A,B, C and D each of mass m are kept at the corners of a square of side L. Now the particle D is taken to infinity by an external agent keeping the other particles fixed at their respective positions . The work done by the gravitational force acting on the particle D During its movement is
View SolutionA particle of mass 5M at rest decays into two particle of masses 2 m and 3 m having non zero velocities. The ratio of de - broglie wavelengh of the particles is
View Solution