A system consists of n identical particles each of mass m. The total number of interaction potential energy terms possible are n(n−1)x. Find value of x.
The correct Answer is:B
To solve the problem, we need to find the value of x in the expression for the total number of interaction potential energy terms possible among n identical particles, which is given as:
n(n−1)x
1. Understanding the Problem:
- We have n identical particles, each with mass m.
- We need to calculate the total number of interaction potential energy terms between these particles.
2. Identifying Interactions:
- Each pair of particles can interact with each other. For n particles, the number of ways to choose 2 particles from n is given by the combination formula C(n,2).
- The formula for combinations is:
C(n,2)=n!2!(n−2)!=n(n−1)2
3. Calculating Total Interactions:
- The total number of interaction potential energy terms is therefore:
Total Interactions=n(n−1)2
4. Setting Up the Equation:
- According to the problem, this total number of interactions is also given by:
n(n−1)x
- We can set the two expressions equal to each other:
n(n−1)2=n(n−1)x
5. Solving for x:
- Since n(n−1) is common on both sides (and assuming n≠0 and n≠1), we can cancel it out:
12=1x
- Cross-multiplying gives:
x=2
Final Answer:
The value of x is 2.
---
- We have n identical particles, each with mass m.
- We need to calculate the total number of interaction potential energy terms between these particles.
- Each pair of particles can interact with each other. For n particles, the number of ways to choose 2 particles from n is given by the combination formula C(n,2).
- The formula for combinations is:
C(n,2)=n!2!(n−2)!=n(n−1)2
- The total number of interaction potential energy terms is therefore:
Total Interactions=n(n−1)2
- According to the problem, this total number of interactions is also given by:
n(n−1)x
- We can set the two expressions equal to each other:
n(n−1)2=n(n−1)x
- Since n(n−1) is common on both sides (and assuming n≠0 and n≠1), we can cancel it out:
12=1x
- Cross-multiplying gives:
x=2
The value of x is 2.
Similar Questions
Knowledge Check
- Question 1 - Select One
A system consits of n identical particles each of mass m. The total number of interactions between particles possible are :
An(n+1)B12n(n+1)Cn(n−1)D12n(n−1) - Question 2 - Select One
The total number of terms in the expansion of (x+y+z+ω)n,n∈N is
A^(n+3)C3B^(n+4)C3C^(n+3)C2D^(n+5)C2
Four particles each of mass m are kept at the four vertices of a square of side 'a' . Find graitational potential energy of this system.
View SolutionEight particles of mass 'm' each are placed at the verties of a cube of side 'a' . Find gravitational potential energy of this system .
 . View Solution
. View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
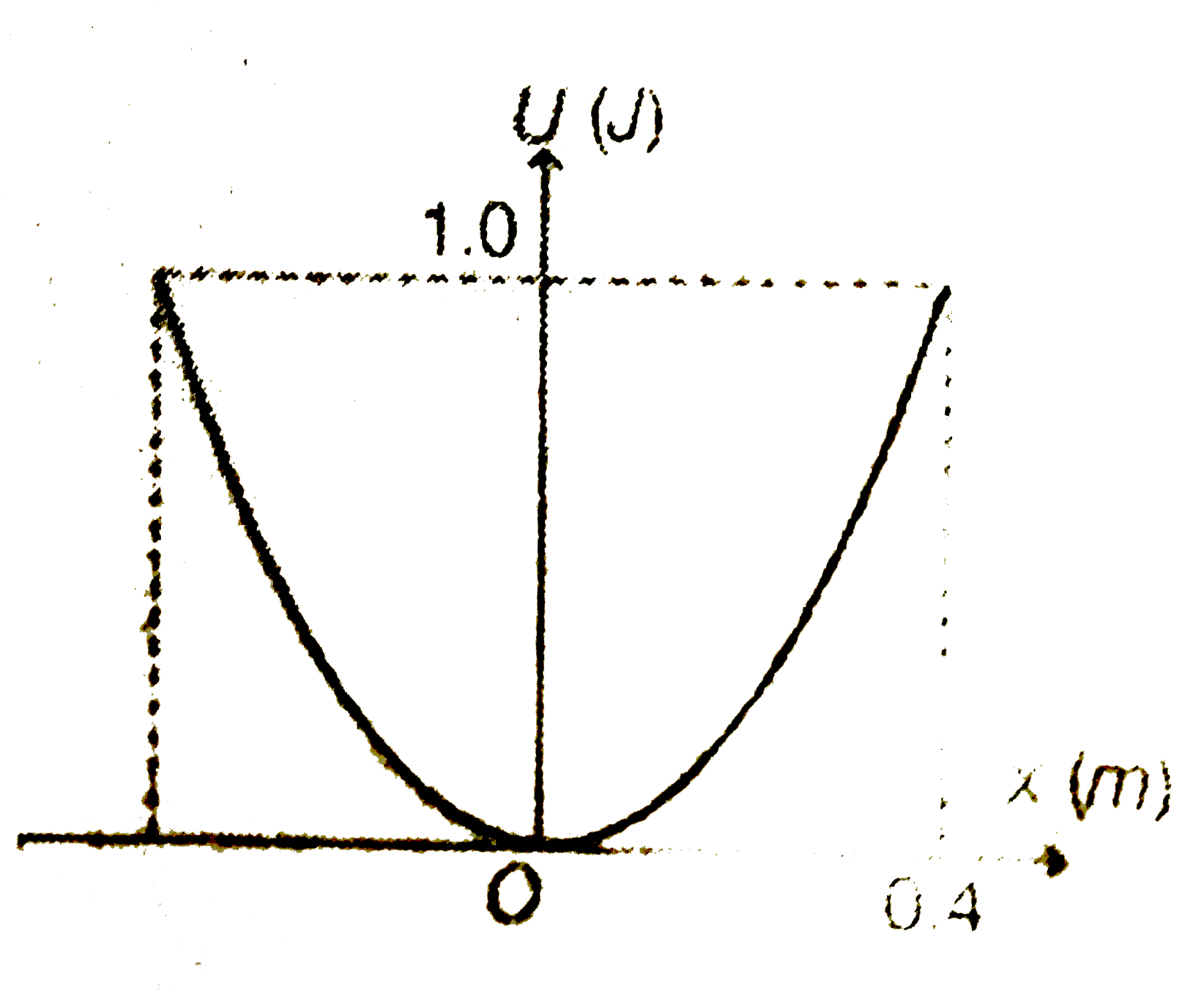 View Solution
View SolutionIf the number of terms in the expansion of (x+y+z)n are 36, then find the value of n.
View SolutionFind the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View SolutionFind the totoal number of distnct or
dissimilar terms in the expansion of
(x+y+z+w)n,n∈NView Solution

