In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by TΔX, where T is temperature of the system and ΔT is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas x=32R h(TTA)+Rh)(VVA). Here, R is gas constant, V is volume of gas, TAand TA are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.
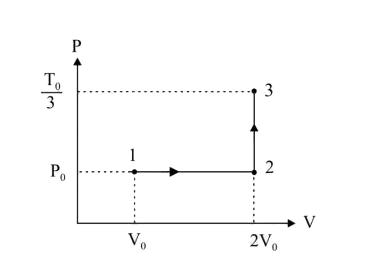
If the process carried out on one mole of monatomic ideal gas is as shown in figure in the PV-diagram with P0V0=13,RT0 , the correct match is :

I→Q,II→R,III→S,IV→U
I→Q,II→R,III→S,IV→U
I→Q,II→S,III→R,IV→U
I→S,II→S,III→Q,IV→T
The correct Answer is:B
1→2 Isothermal process
2→3 Isochoric process
W1→2→3=W1→2=P0(2V0−V0)=P0V0=RT03
U1→2→3=U1→2+U2→3
=32[P2V2−P1V1]+32[P3V3−P2V2]=32P0[2V0−V0]+32[3p02×2V0−p0(2V0)]
=32P0V0+32P0V0=3P0V0=3×RT03=RT0
Q1→2→3=Q1→2+Q2→3
W1→2+Δu1→2+Δu2→3P0V0+32P0V0+32P0V0=4P0V0=4RT03
Q1→2=52P0V0=56RT0
Correct option is (B)
Similar Questions
एक आदर्श एकपरमाणुक गैस के एक ऊष्मागतिकी प्रक्रम में गैस द्वारा अतिसूक्ष्म ऊष्मा का अवशोषण TΔX से दिया गया है , जहाँ T निकाय का तापमान तथा Δx निकाय की एक ऊष्मागतिकी मात्रा X में अतिसूक्ष्म परिवर्तन है । एक मोल एकपरमाणुक आदर्श गैस के लिए X=32Rln(TTA)+Rln(VVA) है । यहाँ , V गैस का आयतन , R नियतांक , TA तथा VA. नियतांक हैं ।
सूची- I एक प्रक्रिया में सम्मिलित कुछ मात्राओं को दर्शाती है । सूची- II में इन्हीं मात्राओं का सम्भावित मान दिया गया है ।

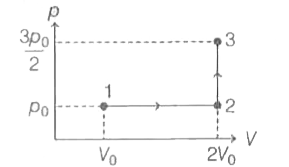
यदि एक मोल एकपरमाणुक आदर्श गैस पर चित्र में दिखाए गए pV- ग्राफ चित्र के अनुसार , जहाँ p0V0=13RT0 , है , प्रक्रम किया जाता है , तब सही मिलान है
View SolutionThe volume of 1 mol of an ideal gas with the adiabatic exponent gamma is changed according to the relation V = b/T where b = constant. The amount of heat absorbed by the gas in the process if the temperature is increased by Delta T will be
View SolutionFor a monatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume is T V^(x) = constant where x is:
View SolutionA monatomic gas undergoes a thermodynamic process such that T∝V−27 (T = temperature and V = volume of the gas) As heat is supplied to the gas, choose INCORRECT option.
View SolutionOne mole of a monoatomic ideal gas undergoes a thermodynamic process such that V^3/T^2 = constant. Then,
View SolutionFor one mole of an ideal gas (δPδT)V(δVδT)P(δVδP)T=
View SolutionThe volume of one mole of an ideal gas with the adiabatic exponent gamma is changed according to the relation V=(a)/(T) where a is a constant. Find the amount of heat absorbed by the gas in the process, if the temperature is increased by Delta T
View SolutionAn ideal gas having pressure p volume V and temperature T and undergoes a thermodynamic ' process in which dw=0 and dQ<0. Then for the gas
View Solution
