A non-conducting thin disc of radius R rotates about its axis with an angular velocity ω. The surface charge density on the disc varies with the distance r from the centre as σ(r)=σ0[1+(rR)β], where σ0 and β are constants. If the magnetic induction at the center is B=(910)μ0σ0ωR, the value of β isSolution in Telugu
14
4
12
2
The correct Answer is:A
Total charge on the disc, Q=σ(πR2)
Period of motion, T=2π/ω
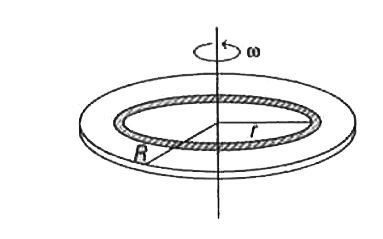
So, current in the ring, dI=dQT
∵ Q=σπR2⇒dQ=2σπrdr
∴ dI=2σπrdr2π×ω=σ rdr
Magnetic fiedl due to ring is
dB=μ0dI2r
So, magnetic field due to disk is
B=∫dB=∫R0μ02r.σω rdr
On putting value of ω, we get
B=μ0σ0ω2∫R0[1+(rR)β]dr
=μ0σ0ω2[R+Rβ+1Rβ(1+β)]=μ0σ0ω2×(2+β1+β)R
Now,
B=910μ0σ0ωR=μ0σ0ωR2×(2+β)(1+β)
⇒ 5β+10=9β+9
⇒ β=14
Topper's Solved these Questions
Similar Questions
A force F is applied in a square plate of length L . If the percentage error in the determination of L is 3% and in F in 4% then permissible error in the calculation of pressure is
02:44View SolutionA tokamak fusion test reactor works on
05:37View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.09:18View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
04:46View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density sigma rotates about its axis with an angular velocity omega . Find : (a) the magnetic induction at the centre of the disc, (b) the magnetic moment of the disc. ( c) the ratio of magnetic moment and angular momentum of disc.
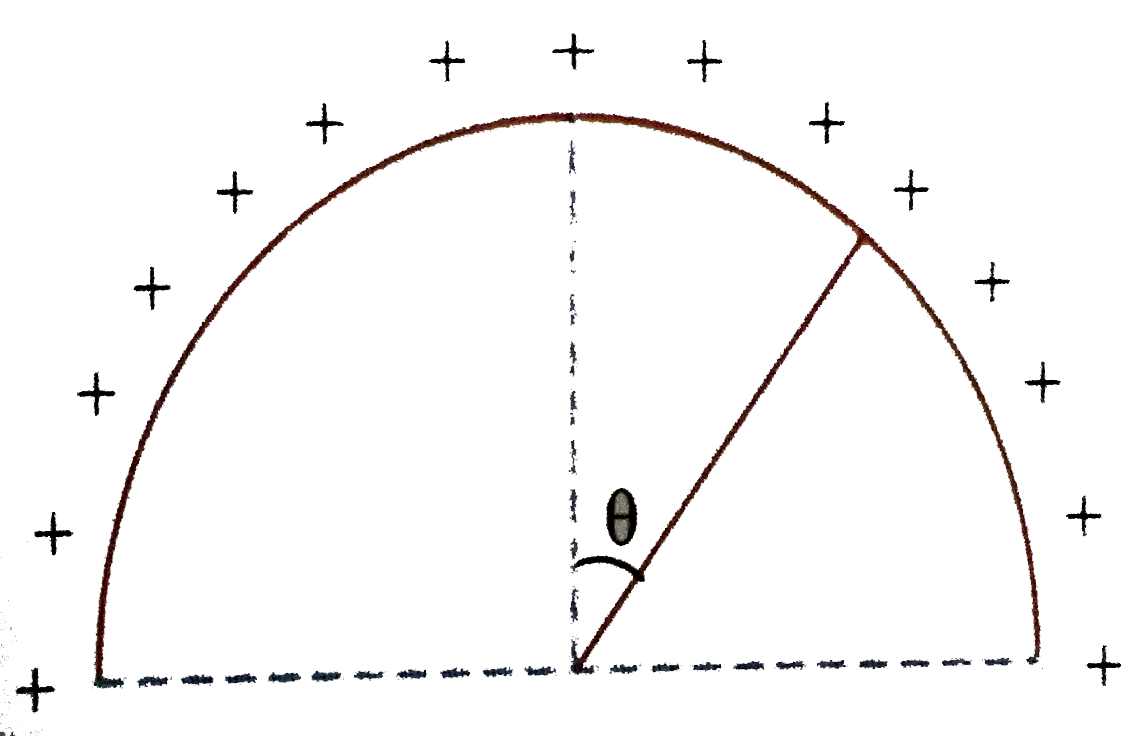
03:31View SolutionFor the hemisphere of radius R shown in the figure the surface charge density σ varies with θ (shown in figure) as σ=σ0cosθ the total charge on the sphere is
 03:10View Solution
03:10View SolutionA flat disc of radius R charged uniformly on its surface at a surface charge density sigma . About its central axis of rotation it rotates at an angular speed omega . Find the magnetic moment of disc due to rotation of charges.
02:58View SolutionA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionIf Σnr=1cos−1xr=0,thenΣnr=1xr equals
08:35View SolutionA non0conducting disk of radius R has surface charge density which varies with distance from the centre as sigma (r ) = sigma _(0)[1+ sqrt((r )/(R ))], where sigma _(0) is a constant. The disc rotates about its axis with angular velocity omega. If B is the magnitude of magnetic induction at the centre, then (B)/(mu_(0) sigma _(o)omega R) will be
09:19View SolutionA non-conducting thin disc of radius R rotates about its axis with an angular velocity ω. The surface charge density on the disc varies with the distance r from the centre as σ(r)=σ0[1+(rR)β], where σ0 and β are constants. If the magnetic induction at the center is B=(910)μ0σ0ωR, the value of β is
View SolutionA circular disc of radius carries surface charge density =sigma_(0)(1-(r )/(R )) , where sigma_(0) is a constant and is the distance from the center of the disc Electric flux through a lange spherical surface that endcloses the charged disc completely is phi_(0) . electric flux through another spherical surface of radius (R ) /(4) and consentri with the disc is phi . Then the ratio (phi_(0))/(phi) is __________.
04:30View SolutionThe surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the centre of the disc σ2∈0. With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc is
04:40View SolutionA disc of radius R rotates with constant angular velocity omega about its own axis. Surface charge density of this disc varies as sigma = alphar^(2) , where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.02:58View Solution

