A non0conducting disk of radius R has surface charge density which varies with distance from the centre as where is a constant. The disc rotates about its axis with angular velocity If B is the magnitude of magnetic induction at the centre, then will be
The correct Answer is:C
Consider an elemental ring of radius r of thickness dr
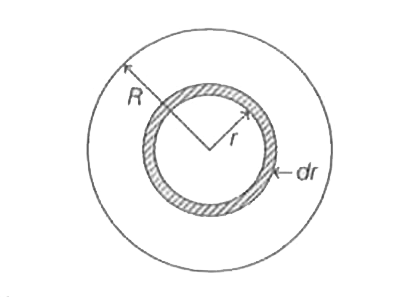
Charge on ring Area of ring Charge density
Current through ring, di as angular velocity of disc is
So,
Now, manetic induction due to elemental ring at thte centre,
As
For magnetic induction due to entire dusc, we integrate from to
IInd part
Topper's Solved these Questions
Similar Questions
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View Solution
Knowledge Check
A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2A non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.
 Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πR
Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πRFor the hemisphere of radius R shown in the figure the surface charge density σ varies with θ (shown in figure) as σ=σ0cosθ the total charge on the sphere is
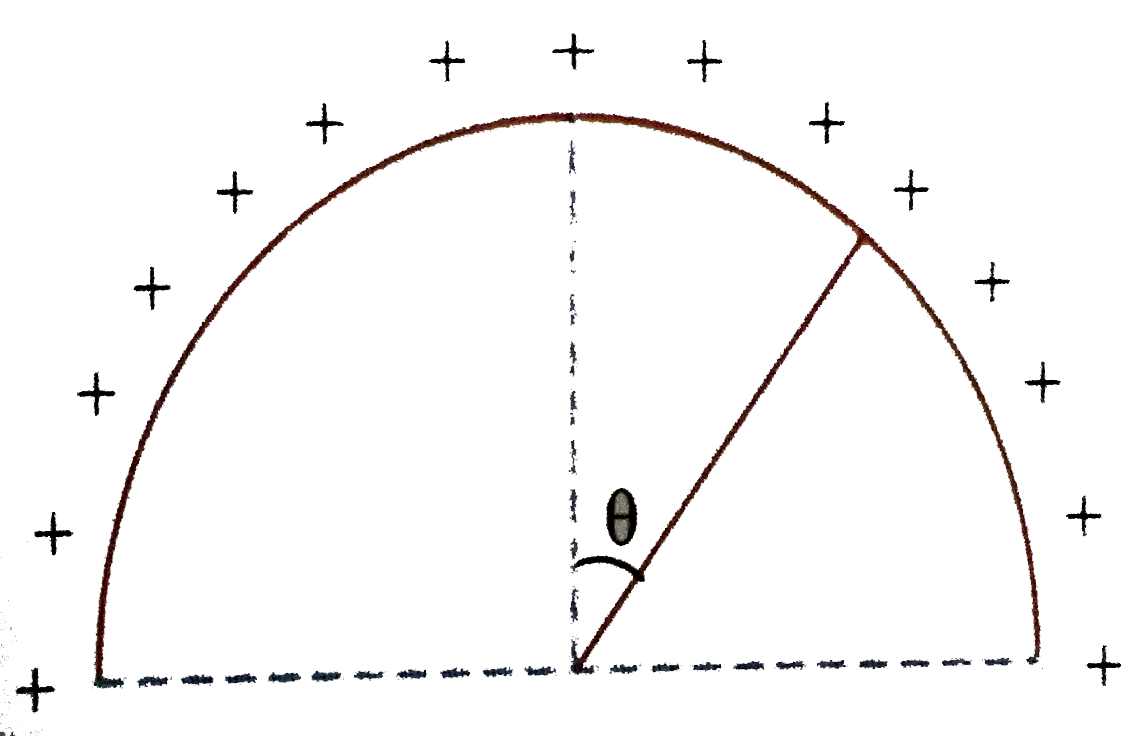 A2σ0πR2Bσ0πR22Cσ0πR23Dσ0πR2
A2σ0πR2Bσ0πR22Cσ0πR23Dσ0πR2
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.

View SolutionA non-homogeneous cylinder of radius "R" carries a current I whose current density varies with the radial "distance "r" from the centre of the rod as J=σr where σ is a constant.The magnetic field at a point "P" at a distance r<R from the centre of the rod is
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density s rotates about its axis with an angular velocity ω. Find
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
View Solution
