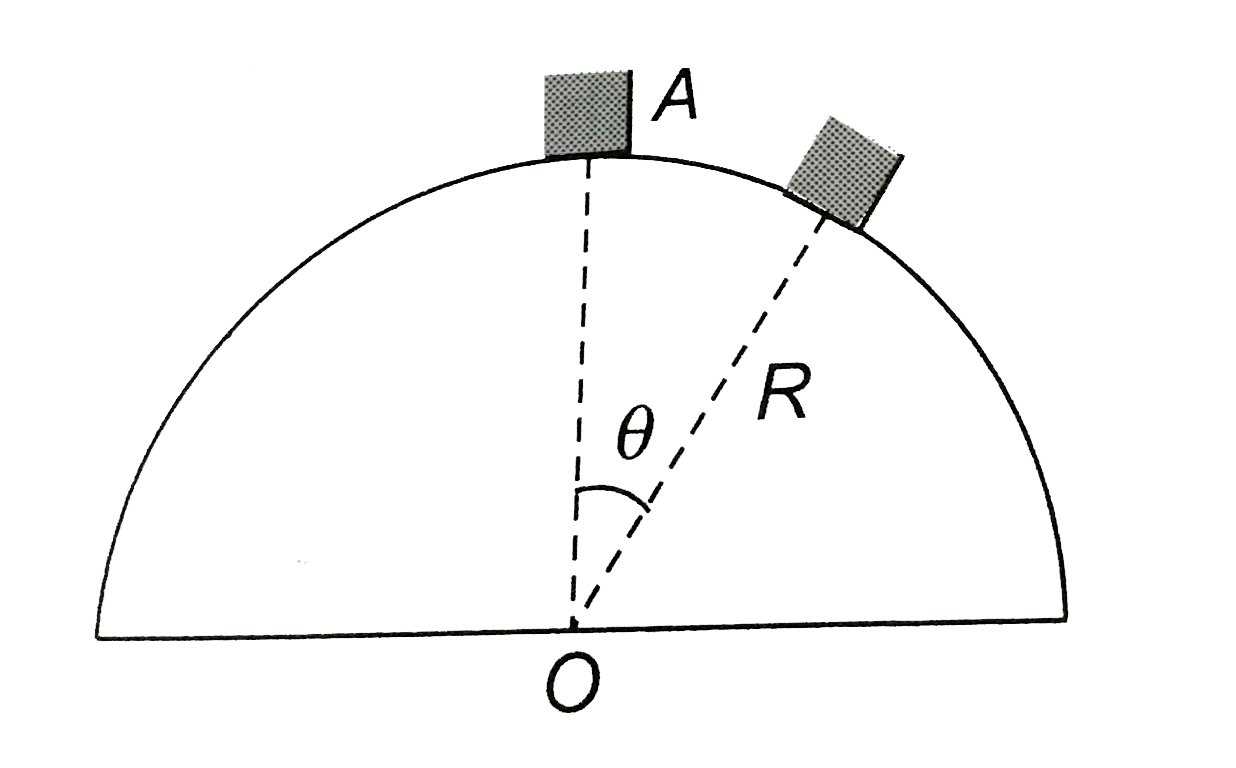
A particle is placed at rest inside a hollow hemisphere of radius 'R'. The co-efficient of friction between the particle and the hemisphere is μ=1√3 The maximum height upto which the particle can remain stationary is .
R2
(1−√32)R
√32R
3R8.
The correct Answer is:B
Given
Radius of hollow hemisphere = R
Coefficient of frication (μ)=1√3.
hmax=[1−1√μ2+1]R.
=⎡⎢
⎢
⎢
⎢⎣1−1√(13)2+1⎤⎥
⎥
⎥
⎥⎦×R
=⎡⎢
⎢⎣1−1√13+1⎤⎥
⎥⎦×R
hmax=[1−√32]R.
Topper's Solved these Questions
- EAMCET -2016 (AP)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (AP)EXERCISE - CHEMISTRY
3 Videos
- EAMCET -2016 (AP)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (AP)EXERCISE - CHEMISTRY
3 Videos
- EAMCET - 2018 (TS) SHIFT - 2BOOK - SIA PUBLICATIONCHAPTER - EAMCET - 2018 (TS) SHIFT - 2EXERCISE - Chemistry
18 Videos
- EAMCET -2016 (TS)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (TS)EXERCISE - CHEMISTRY
36 Videos
Similar Questions
If the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View Solution
Knowledge Check
A partical is placed at rest inside a hollow hemisphare of redius R. The coefficient of friction between the partical and the homisphere is μ=1√3. The maximum height up to which the partical can remain stationary is
AR2B(1−√32)RC√32RD3R8The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is
Ar√1+μ2Br[1−1√1+μ2]Cr√1+μ2Dr[√1+μ2−1]A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
If the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View SolutionA particle is dropped from rest from a height h0 on a horizontal floor. The coefficient of restitution between the floor and particle is e. Maximum height attained by the particle after first rebound is
View SolutionA particle is dropped from rest from a height h0 on a horizontal floor. The coefficient of restitution between the floor and particle is e. Maximum height attained by the particle after first rebound is
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be
View Solution
