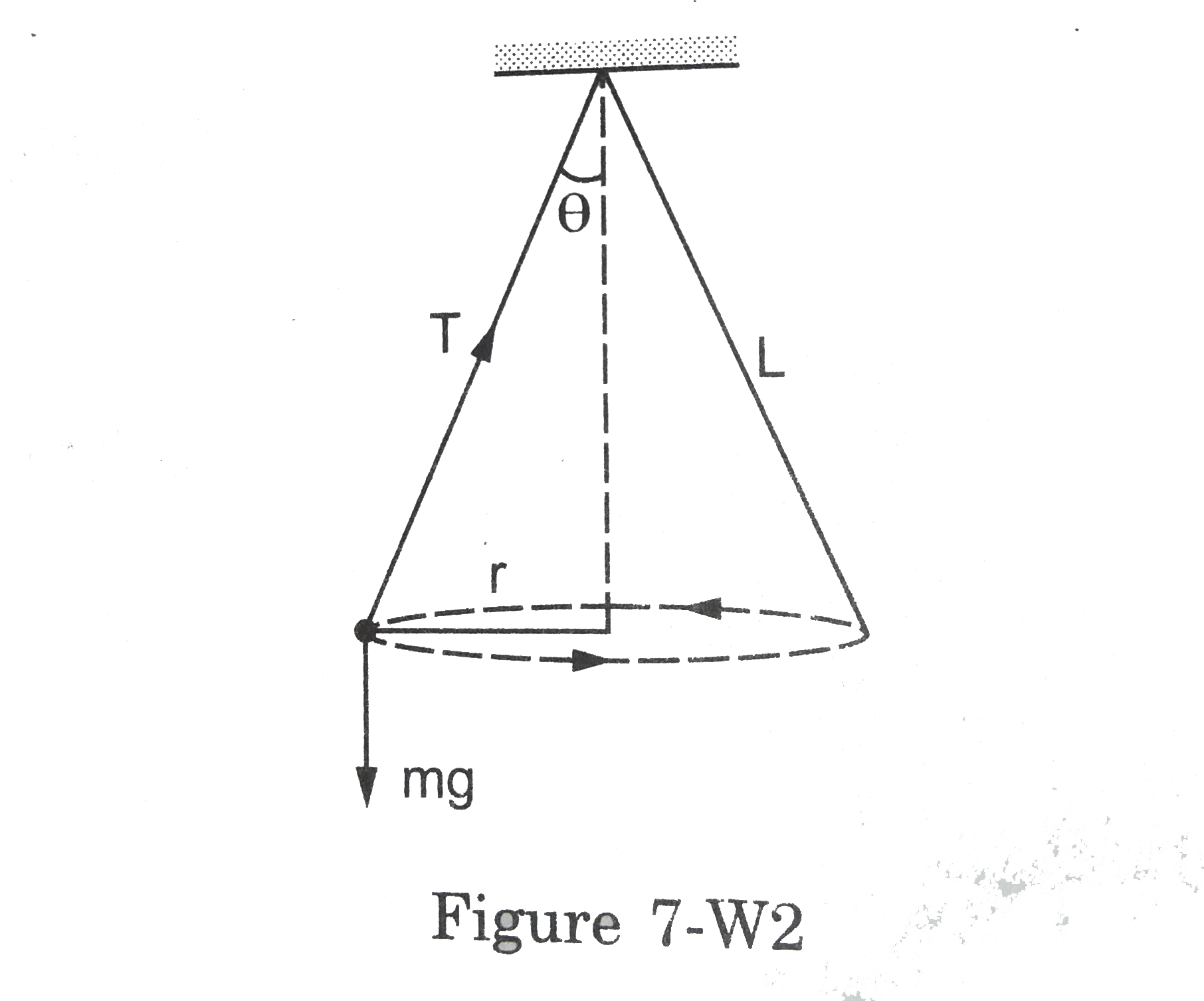
A particle of mass 'm' is suspended from a ceiling through a string of length 'L'. If the particle moes in a horizontal circle of radius 'r' as shown in the figure , then the speed of the particle is
 .
.
r√g√L2−r2
r√r√L2−r2
r√gL2−r2.
g√rL2−r2.
The correct Answer is:A
 .
.
from above diagram
Tsinθ=mv2r
Tcosθ=mg
Dividing equation (1) by equation (2) , we get
TsinθTcosθ=mv2rmg
tanθ=v2rg.
From above diagram
tanθ=r√L2−r2
From equation (iii) tanθ=v2rg, we get
v2rg=r√L2−r2.
v=r√g√L2−r2.
Topper's Solved these Questions
- EAMCET -2016 (AP)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (AP)EXERCISE - CHEMISTRY
3 Videos
- EAMCET -2016 (AP)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (AP)EXERCISE - CHEMISTRY
3 Videos
- EAMCET - 2018 (TS) SHIFT - 2BOOK - SIA PUBLICATIONCHAPTER - EAMCET - 2018 (TS) SHIFT - 2EXERCISE - Chemistry
18 Videos
- EAMCET -2016 (TS)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (TS)EXERCISE - CHEMISTRY
36 Videos
Similar Questions
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View Solution
Knowledge Check
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
.Av=r√g(L2−r2)14andT=mgL(L2−r2)12Bv=r2√g(L3−r3)14andT=mgL(L2−r2)12Cv=r√g(L2−r2)14andT=mgL2(L2−r2)12Dv=r√g(L2−r2)14andT=mgL(L2−r2)14A paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronly
AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronly
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionConsider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

View SolutionA particle of mass 'm' and charge 'q' is suspended from the ceiling with the help of an insulating wire of length 'l'. It is placed in an uniform electric field as shown in figure. Then the time period of oscillation is
_2019_CBT6_E01_041_Q01.png)
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle of mass 'm' and charge 'q' is suspended from the ceiling with the help of an insulating wire of length 'l'. It is placed in an uniform electric field as shown in figure. Then the time period of oscillation is
_2019_CBT6_E01_041_Q01.png)
View Solution
