The function f (x) is defined as follows :
f(x)=2−3x when x<0=3x−2 when x≤0
Evaluate limx→0+f(x)andlimx→0−f(x) and hence state whetherlimx→0f(x) exists or not .
Text Solution
The correct Answer is:(−2),2 and does not exist
|
Topper's Solved these Questions
- LIMITBook:CHHAYA PUBLICATIONChapter:LIMITExercise:EXERCISE 2 ( Long Answer Type Questions)
Explore 38 Videos
- LIMITBook:CHHAYA PUBLICATIONChapter:LIMITExercise:Sample Questions for Competitive Exams (Multiple Correct Answers Type )
Explore 5 Videos
- LIMITBook:CHHAYA PUBLICATIONChapter:LIMITExercise:EXERCISE 2 (Very Short Answer Type Questions )
Explore 56 Videos
- LAWS OF INDICESBook:CHHAYA PUBLICATIONChapter:LAWS OF INDICESExercise:Long Answer Type Questions
Explore 6 Videos
- LINEAR DIFFERENTIAL EQUATION Book:CHHAYA PUBLICATIONChapter:LINEAR DIFFERENTIAL EQUATION Exercise:Sample Question for Competitive Examination(E. Assertion-Reason Type)
Explore 2 Videos
Similar Questions
Knowledge Check
Let f(x)={1when x is rational0when x is irrational' then limx→0f(x) is :
A0B1C12Dnone of these
If f(x) is defined as follows:
f(x)⎧⎪⎨⎪⎩1x>0−1x<00x=0
Then show that limx→0f(x) does not exist.
View SolutionIf f(x) is defined as
f(x)={2x+3x≤03x+3x≥0
then evaluate : limx→0f(x)andlimx→1f(x)
View SolutionIf f(x) is defined as follows:
f(x)=⎧⎪⎨⎪⎩1x>0−1x<00x=0
Then show that limx→0f(x) does not exist.
View SolutionEvaluate limx→0f(x), where
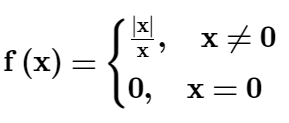
View SolutionEvaluate limx→0f(x), where
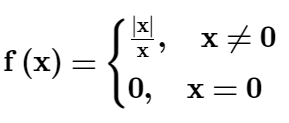
View SolutionIf f(x)=|x|x, then show that limx→0f(x) does not exist.
View SolutionIf f(x)=|x|x, then show that limx→0f(x) does not exist.
View Solution
