The locus of the centere of a circle which passes through the point (0,0) and cuts off a length 2b from the line x=c is-
A
y2+2cx=b2+c2
B
x2+cx=b2+c2
C
y2+2cy=b2+c2
D
none of these
Video Solution
Text Solution
The correct Answer is:A
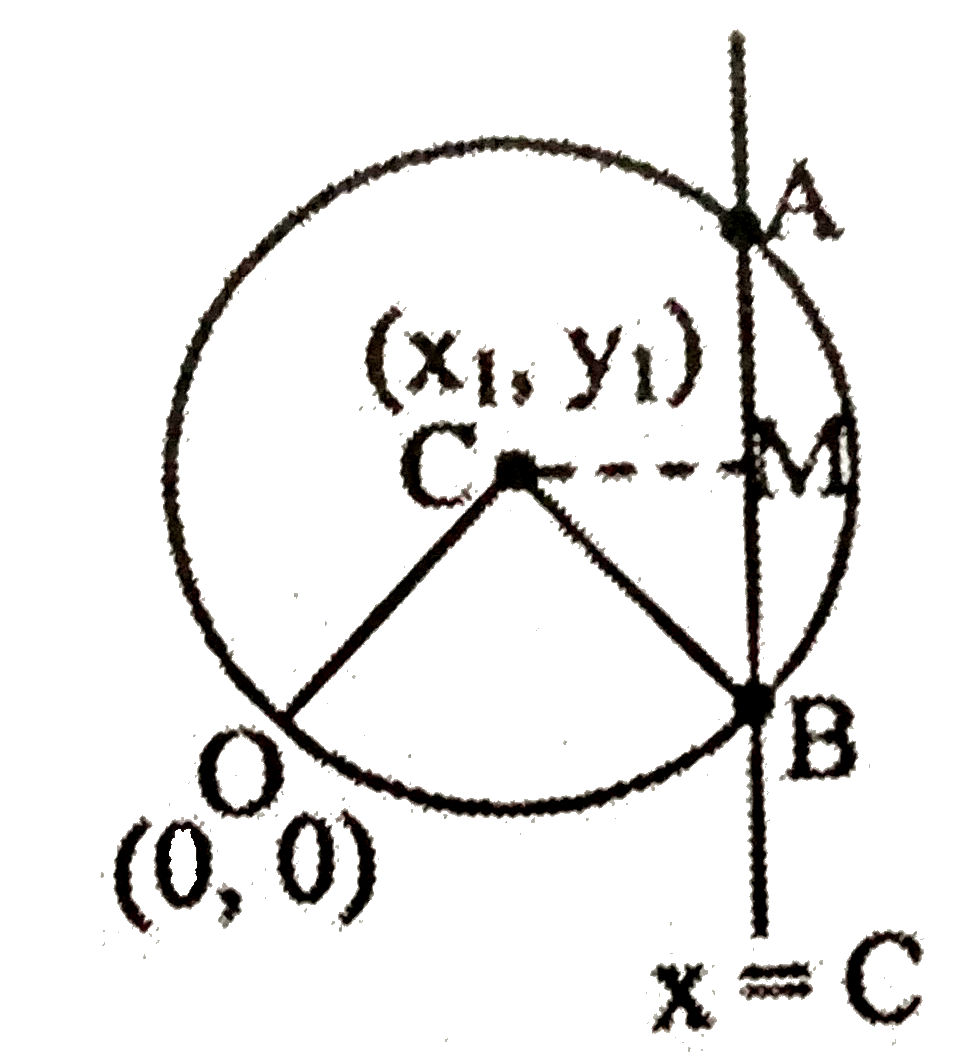
Let the centre of circle
C(x1,y1)
As it passes through (0,0)
its radius OC=√(x21−y21)
CB=r=√x21−y21
CM= length of ⊥ from C on line x-c=0
CM∣∣∣x1−c√1∣∣∣
in ΔBCM
⇒b2=CB2−CM2
⇒b2=x21+y21−(x1−c)2
⇒∴ locus y2+2cx=b2+c2
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Locus of the centre of the circle which always passes through the fixed points (a,0) and (-a,0) is
Ax = 1Bx + y = 6Cx + y = 2aDx = 0The length of the diameter of the circle which passes through the point (2,3) and touches the x-axis at the point (1,0) is
A53B65C103D35Equation to the circles which pass through the point (2,3) and cut off equal chords of length 6 units along the lines y-x-1=0 and y+x-5=0 is
A(x−3)2+(y−2√3)2=(3√2)2B(x−2)2+(y−3−3√2)2=(3√2)2C(x−2√3)2+(y−3)2=(3√2)2Dnone of these
The radius of the circles which pass through the point (2,3) and cut off equal chords of length 6 units along the lines y-x-1=0 and y+x-5=0 is r then [r] is (where [.] denotes greatest integer function)
View SolutionFind the equation of the circle , which passes through the origin and cuts off intercepts a and b from the axes.
View SolutionIn how many ways can the letters of the word PENCIL be arranged so that (i) N is always next to E ? (ii) NandE are always together? .
View SolutionIf a circle passes through the point (0,0),(a,0)and(0,b) , then find its center.
View SolutionFind the equation of the circle which passes through the origin and cut off equal chords of √2 units from the lines y=xandy=−x.
View Solution
