The orbital velocity of a satellite at point B with radius rB is v. The radius of a point A is rA. If the orbit is increased in radial distance so that rA becomes 1.2rA find the orbital velocity at (1.2rA):
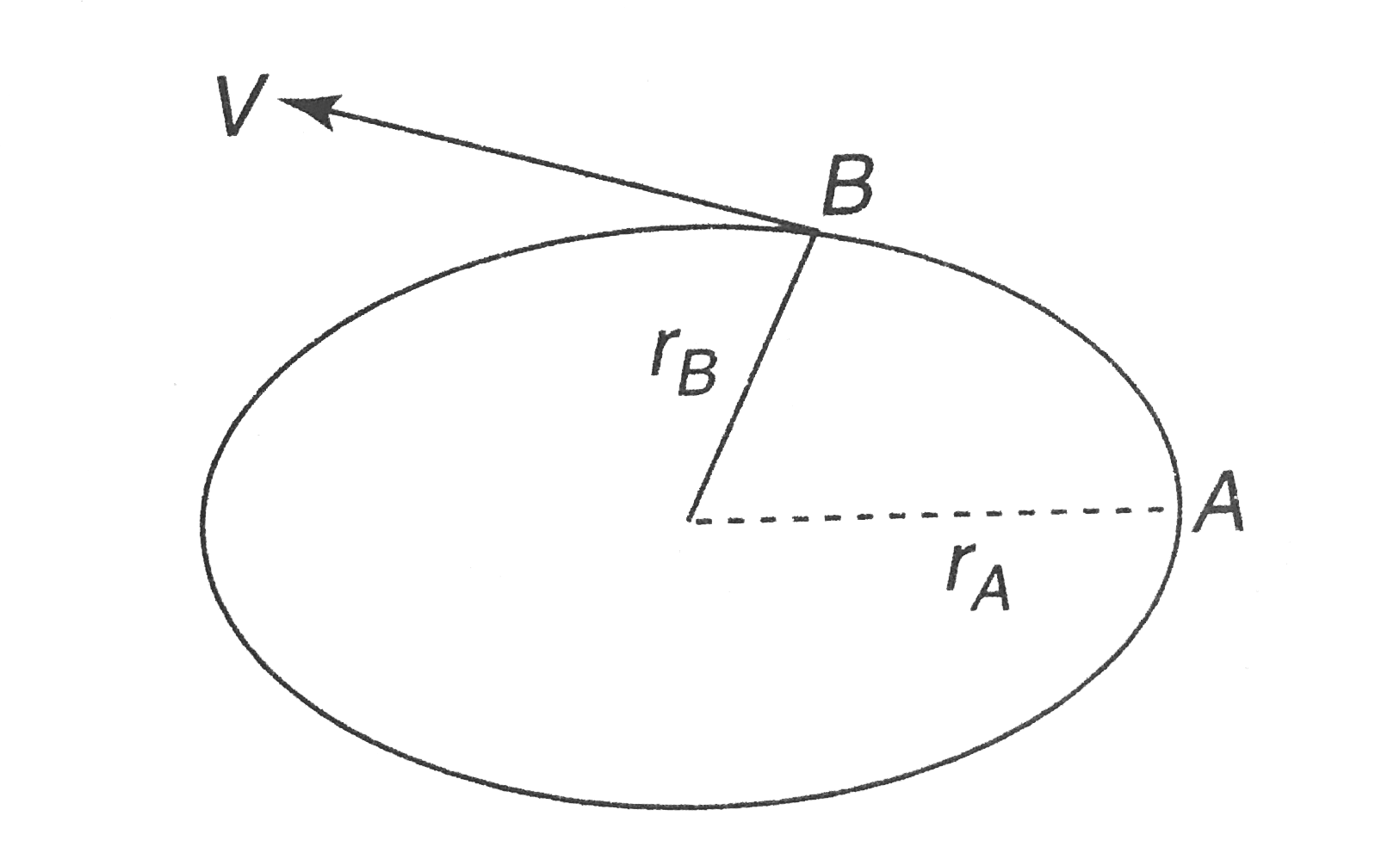
vrBrA√1.2
vrA1.2rB
vrB1.2rA
vrArB√1.2
The correct Answer is:A
Using principle of anguklar momentum
L=mvATA=mvrB
vA=vrBrA,v=√GMr
vovA=(rA1.2rA)1.2⇒vo=vrsrA√(1.2)
Topper's Solved these Questions
Similar Questions
The period of revolution of a satellite in an orbit of radius 2R is T. What will be its period of revolution in an orbit of radius 8R ?
View SolutionThe time period of a satellite in a circular orbit of radius R is T. The period of another satellite in a circular orbit of radius 9R is :
View Solution
Knowledge Check
The orbital velocity of a satellite at point B with radius rB and n. The radius of a point A is rA. If the orbit is increased in radial distance so that rA becomes .12rA find the orbital velocity at (1.2rA):
 AvrBrA√1.2BvrA1.2rBCvrB1.2rADvrArB√2
AvrBrA√1.2BvrA1.2rBCvrB1.2rADvrArB√2The binding of a satellite of mass m in a orbit of radius r is
AmgR2rBmgR22rC−mgR3rD−mgR32rThe velocity of a satellite moving in an orbit about earth at a distance equal to radius R of earth will be
A√gRB√0.5gRC√2gRD√3gR
The velocity of a satellite moving in an orbit about earth at a distance equal to radius R of earth will be
View SolutionThe time period of a satellite in a circular orbit of radius R is T. The radius of the orbit in which time period is 8 T is
View SolutionIf the orbital velocity of a planet is given by v=GaMbRc then
View SolutionThe radius of the orbit of a satellite is r and its kinetic energy is k if the radius of the orbit is doubled then the new kinetic energy k is
View SolutionThe period of a satellite in a circular orbit of radius R is T. The period of another satellite in circular orbit of radius 4 R is :
View Solution
