A pendulam of length L and bob of mass M has a speing of force constant K connected a speing of force constsnt K connected horizontally to it at a distance h below is point of suspension. The rod is in equilibrium in vertical podition. The rod of length L. used for vertical suspension s rigid and massless. The frequency of vibration of the system for small values of θ is

12πL√gL+khm
12πL√mgL+km
2π√kL2mgL+kh
12πL√gL+kh2m
The correct Answer is:D
T=[mgLsinθ+kh2θ]
For small angle sin θ≈θ
T=lα=−(mgL+kh2)θ
α=−(mgL+kh2)θ/mL2
Sof=12πL√gL+kh2m
Topper's Solved these Questions
Similar Questions
A simple pendulum of length L and mass m has a spring of force constant k connected to it at a distance h below its point of suspension. Find the frequency of vibrations of the system for small values of amplitude.

View SolutionA simple pendulum of length L and mass m has a spring of force constant k connected to it at a distance h below its point of suspension. Find the frequency of vibrations of the system for small values of amplitude.

View Solution
Knowledge Check
A simple pendulam of length L carriers a bob of mass m. When the bob is at its lowest position, it is given the minimum horizontal speed necessary for it to move in a vertical circle about the point of suspension. When the string is horizontal the net force on the bob is
A√10mgB√5mgC4 mgD1 mgA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 Amg/2B2mgCmg/2√3D√3mg
Amg/2B2mgCmg/2√3D√3mgA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
AmL√2gLBmL√gLCmL√3gLDnone
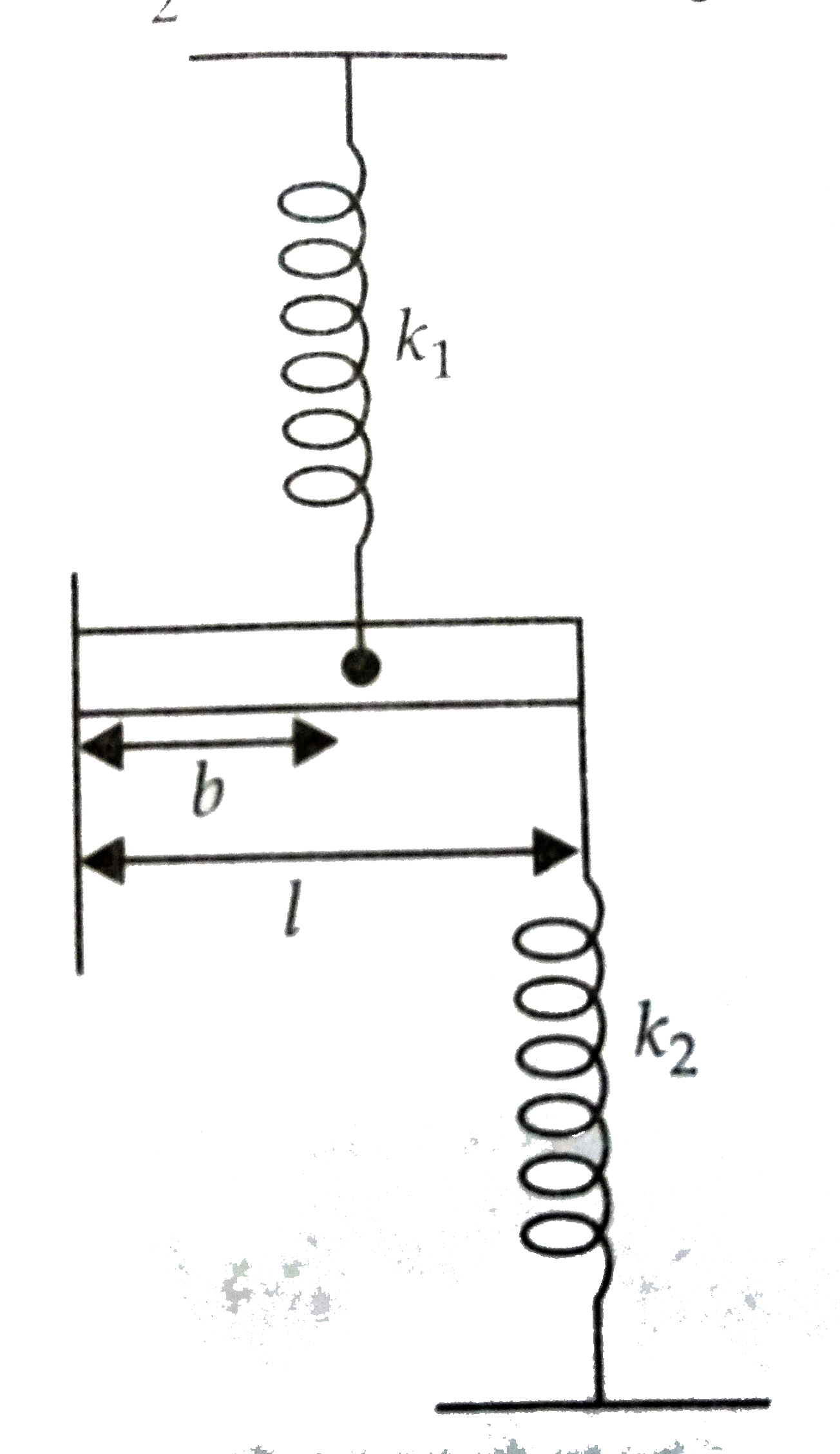
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View Solution
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:

View SolutionA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View Solution
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
View Solution
