Binary stars of comparable masses rotates under the influence of each other's gravity at a distance 2[Gω2]1/3 where ω is the angular velocity of each of the system. If difference between the masses of two stars is 6 units. Find the ratio of the masses of smaller to bigger star.
![Binary stars of comparable masses rotates under the influence of each other's gravity at a distance 2[(G)/(omega^(2))]^(1//3) where omega is the angular velocity of each of the system. If difference between the masses of two stars is 6 units. Find the ratio of the masses of smaller to bigger star.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/A2Z_XI_C08_E01_148_Q01.png)
14:10
1:7
2:8
3:9
The correct Answer is:B
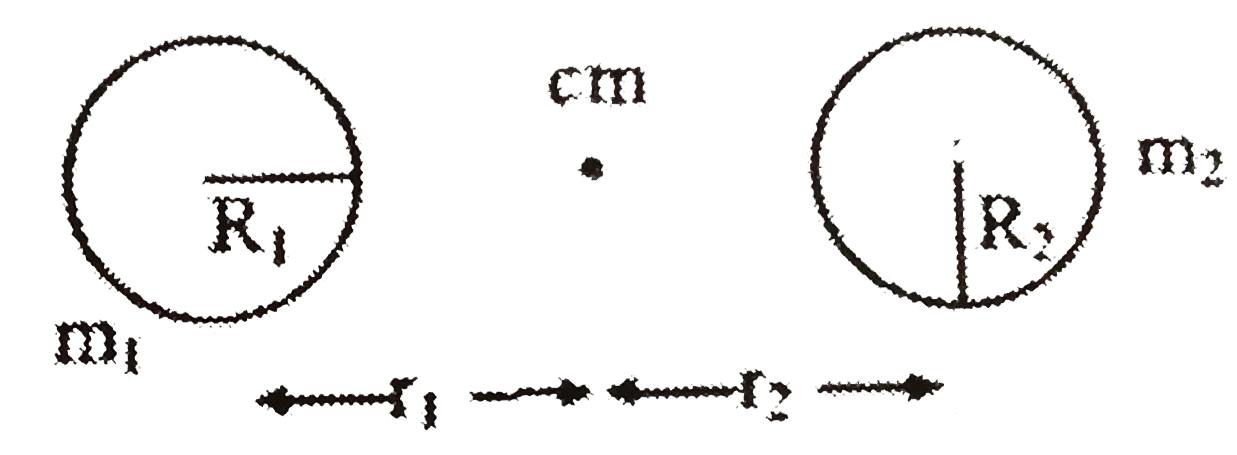
m1r1=m2r2
m1r1ω2=Gm1m2r2
on solving
r=[G(m1+m2)ω2]1/3
on comparing
r=2[Gω2]1/3
(m1+m2)1/3=2
m2−m1=6
m1m2=17
Topper's Solved these Questions
Similar Questions
Binary stars rotate under mutual gravitational force at separation 2(Gω2)13, where ω is the angular velocity of each of the star about centre of mass of the system. If difference between the mass of stars is 6 units. Find the ratio of mass of bigger star to smaller star.
View SolutionBinary stars of comparable masses m1 and m2 rotate under the influence of each other's gravity with a time period T. If they are stopped suddenly in their motions, find their relative velocity when they collide with each constant of gravitation.
View Solution
Knowledge Check
A gramophone record of mass M and radius R is rotating at an angular velocity ω A coin of mass is gently placed on the record at a distance r=R2 from its centre. The new angular velocity of the system is
A2ωM(2M+m)B2ωM(M+2m)CωDωMmIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
ABoth stars have same angular momentum about common centre of massBBoth stars have angular momentum of same magnitude about common centre of massCBoth stars have same angular speedsDBoth stars have same linear speedsA pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The ratio of kinetic energies of the two stars (Km/KM) is .A1B2C4D9
The two components of Procyon have a separation of 4.55'' and period o 40.6 uears. If the distance of the binary is 11.3 light years, calculate the sum of the masses of the two stars in solar units. If the ratio of their masses is 3:1, find the mass of each star.
View SolutionAngular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
View SolutionAngular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
View SolutionIn a double star system, two stars of masses m1 and m2 separated by a distance x rotate about their centre of mass. Find the common angular velocity and Time period of revolution.
View SolutionThe small dense stars rotate about their common centre of mass as a binary system, each with a period of 1 year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is r and the distance of the earth from the Sun is R, find the relation between r and R.
View Solution
