A body of mass √3 kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30° with the vertical. The value of F and tension in the string are.
9.8 JN, 9.8 N
9.8 N, 19.6 N
19.6 N, 19.6 N
19.6 N, 9.8 N
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the body suspended by the string when it is pulled horizontally, causing the string to make an angle of 30° with the vertical.
1. Identify the Forces Acting on the Body:
- The weight of the body (W) acting downwards:
W=mg=√3kg×g
where g=9.8m/s2.
- The tension (T) in the string acting at an angle of 30° with the vertical.
- The horizontal force (F) pulling the body.
2. Calculate the Weight of the Body:
W=√3×9.8=9.8√3N
3. Resolve the Tension into Components:
- The vertical component of the tension (T) balances the weight:
Tcos(30°)=W
- The horizontal component of the tension (T) balances the applied force (F):
Tsin(30°)=F
4. Substituting the Values:
- We know that cos(30°)=√32 and sin(30°)=12.
- Thus, the equations become:
T⋅√32=9.8√3
T⋅12=F
5. Solving for Tension (T):
- From the first equation:
T=9.8√3√32=9.8×2=19.6N
6. Finding the Applied Force (F):
- Substitute the value of T into the second equation:
F=T⋅12=19.6⋅12=9.8N
Final Results:
- The applied force F is 9.8N.
- The tension T in the string is 19.6N.
Summary:
- The values of F and T are 9.8N and 19.6N, respectively.
---
- The weight of the body (W) acting downwards:
W=mg=√3kg×g
where g=9.8m/s2.
- The tension (T) in the string acting at an angle of 30° with the vertical.
- The horizontal force (F) pulling the body.
W=√3×9.8=9.8√3N
- The vertical component of the tension (T) balances the weight:
Tcos(30°)=W
- The horizontal component of the tension (T) balances the applied force (F):
Tsin(30°)=F
- We know that cos(30°)=√32 and sin(30°)=12.
- Thus, the equations become:
T⋅√32=9.8√3
T⋅12=F
- From the first equation:
T=9.8√3√32=9.8×2=19.6N
- Substitute the value of T into the second equation:
F=T⋅12=19.6⋅12=9.8N
- The applied force F is 9.8N.
- The tension T in the string is 19.6N.
- The values of F and T are 9.8N and 19.6N, respectively.
Similar Questions
A mass 'M' is suspended by a rope from a rigid support. It is pulled horizontally with a force F. If the rope makes an angle ' θ' with vertical in equilibrium, then the tention in the string is
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionA small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle '/theta' with the vertical in equilibrium. Then the tension in the string is :
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.

View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
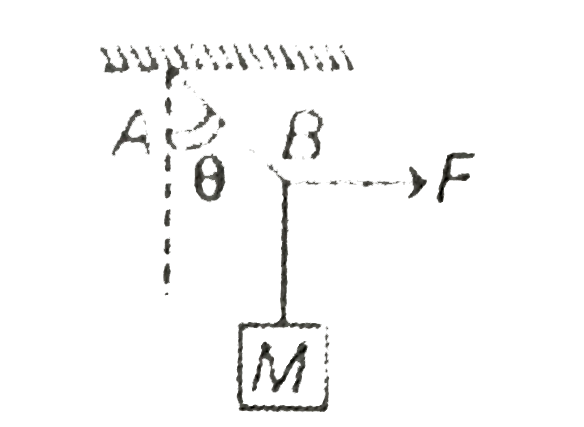
View SolutionA body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View SolutionA body of weight W is suspended by a string It is pulled aside with a horizontal force of 2W and held at rest. The tension in it is
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View Solution
