Space between the plates of a parallel plate capacitor is filled with a dielectric whose dielectric constant varies with distance as per the relation: K(X)=K0+λX,
(λ= constant, K0= constant, X is perpendicular distance from one plate to a point inside dielectric). The capacitance C1 of this capacitor, would be related to its vacuum capacitance C0 per the relation (d = plate separation):
C=λdln(1+K0λd)C0
C=λd.ln(1+K0λd)C0
C=λdln(1+λd/K0)C0
C=λd.ln(1+K0/λd)C0
The correct Answer is:C
To find the capacitance C1 of a parallel plate capacitor filled with a dielectric whose dielectric constant varies with distance, we can follow these steps:
Step 1: Understand the relationship of capacitance with dielectric
The capacitance C of a parallel plate capacitor filled with a dielectric is given by:
C=Kϵ0Ad
where K is the dielectric constant, ϵ0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
Step 2: Define the varying dielectric constant
In this case, the dielectric constant K(x) varies with distance x as:
K(x)=K0+λx
where K0 is a constant and λ is a constant that describes how the dielectric constant changes with distance.
Step 3: Set up the integral for capacitance
To find the total capacitance C1, we need to consider the varying dielectric constant across the distance d. The capacitance can be expressed in terms of an integral:
1C1=∫d0dxK(x)ϵ0A
Substituting K(x):
1C1=∫d0dx(K0+λx)ϵ0A
Step 4: Solve the integral
The integral can be simplified:
1C1=1ϵ0A∫d0dxK0+λx
This integral can be solved using the natural logarithm:
∫dxK0+λx=1λln(K0+λx)
Evaluating from 0 to d:
1C1=1ϵ0A(1λln(K0+λd)−1λln(K0))
=1ϵ0Aλ(ln(K0+λd)−ln(K0))
=1ϵ0Aλln(K0+λdK0)
Step 5: Express C1 in terms of C0
Now, we can express C1:
C1=ϵ0Aλln(K0+λdK0)
The vacuum capacitance C0 is given by:
C0=ϵ0Ad
Thus, we can relate C1 to C0:
C1=C0⋅λdln(K0+λdK0)
Final Result
The capacitance C1 of the capacitor filled with a dielectric whose dielectric constant varies with distance is given by:
C1=C0⋅λdln(K0+λdK0)
The capacitance C of a parallel plate capacitor filled with a dielectric is given by:
C=Kϵ0Ad
where K is the dielectric constant, ϵ0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
In this case, the dielectric constant K(x) varies with distance x as:
K(x)=K0+λx
where K0 is a constant and λ is a constant that describes how the dielectric constant changes with distance.
To find the total capacitance C1, we need to consider the varying dielectric constant across the distance d. The capacitance can be expressed in terms of an integral:
1C1=∫d0dxK(x)ϵ0A
Substituting K(x):
1C1=∫d0dx(K0+λx)ϵ0A
The integral can be simplified:
1C1=1ϵ0A∫d0dxK0+λx
This integral can be solved using the natural logarithm:
∫dxK0+λx=1λln(K0+λx)
Evaluating from 0 to d:
1C1=1ϵ0A(1λln(K0+λd)−1λln(K0))
=1ϵ0Aλ(ln(K0+λd)−ln(K0))
=1ϵ0Aλln(K0+λdK0)
Now, we can express C1:
C1=ϵ0Aλln(K0+λdK0)
The vacuum capacitance C0 is given by:
C0=ϵ0Ad
Thus, we can relate C1 to C0:
C1=C0⋅λdln(K0+λdK0)
The capacitance C1 of the capacitor filled with a dielectric whose dielectric constant varies with distance is given by:
C1=C0⋅λdln(K0+λdK0)
Similar Questions
The area of the plates of a parallel plate capacitor is A and the gap between them is d. The gap is filled with a non homogeneneous dielectric whose dielectric constant varies with the distance ‘y’ from one plate as: K=λsec(πy2d), whereλis a dimensionless constant. The capacitance of this capacitor is
View SolutionThe gap between the plates of a parallel plate capacitor having square plate of edge a and plate separation d is filled with a dielectric of dielectric constant K .K varies parallel to an edge as K=K0−ax where k and a are positive constants and x is the distance from one end.The value of alpha for which capacitor behaves as a capacitor of zero capacitance will be
View Solution
Knowledge Check
If the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
AIncreases by a factor 2BIncreases by a factor √2CDecreased by a factor √2DDecreased by a factor 1/2If the distance between the plates of parallel plate capacitor is halved and the dielectric constant of dielectric is doubled, then its capacity will
Aincrease by 16 timesBincrease by 4 timesCincrease by 2 timesDremain the sameIn figure half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
 A
A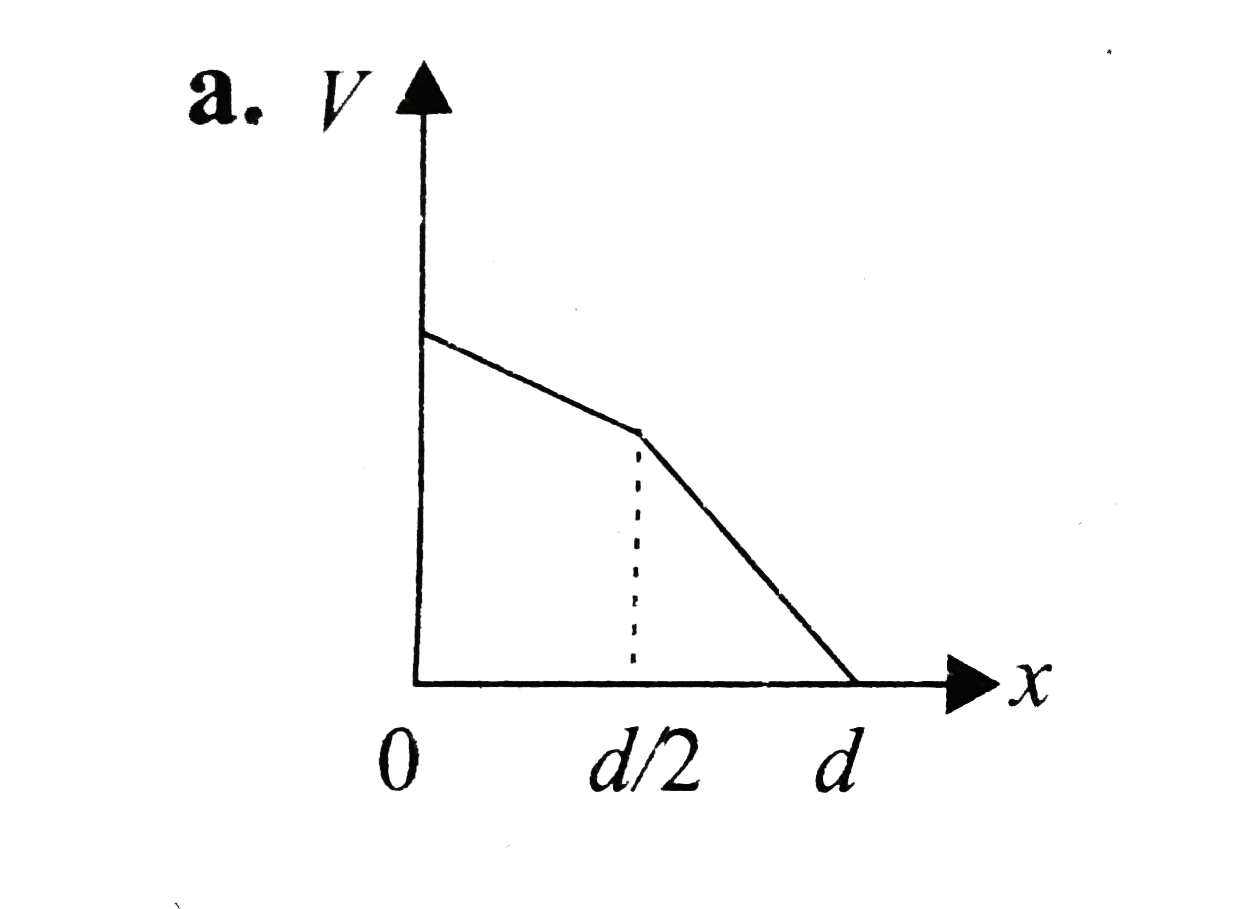 B
B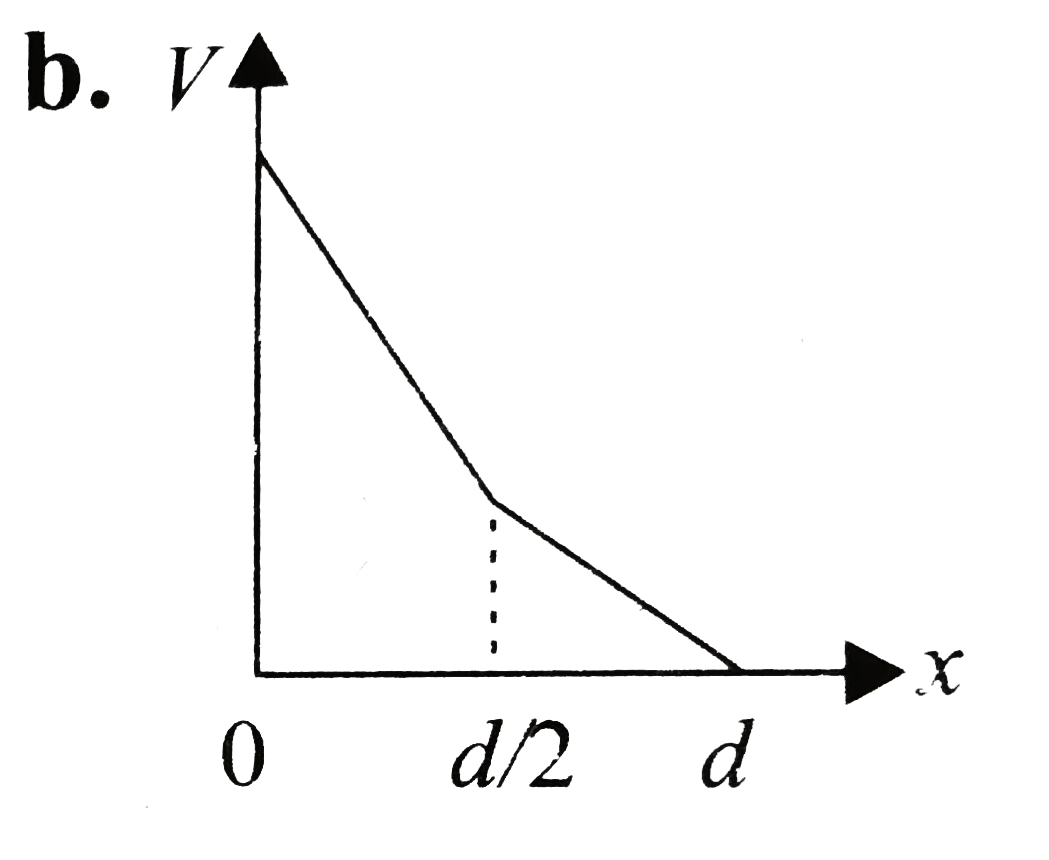 C
C D
D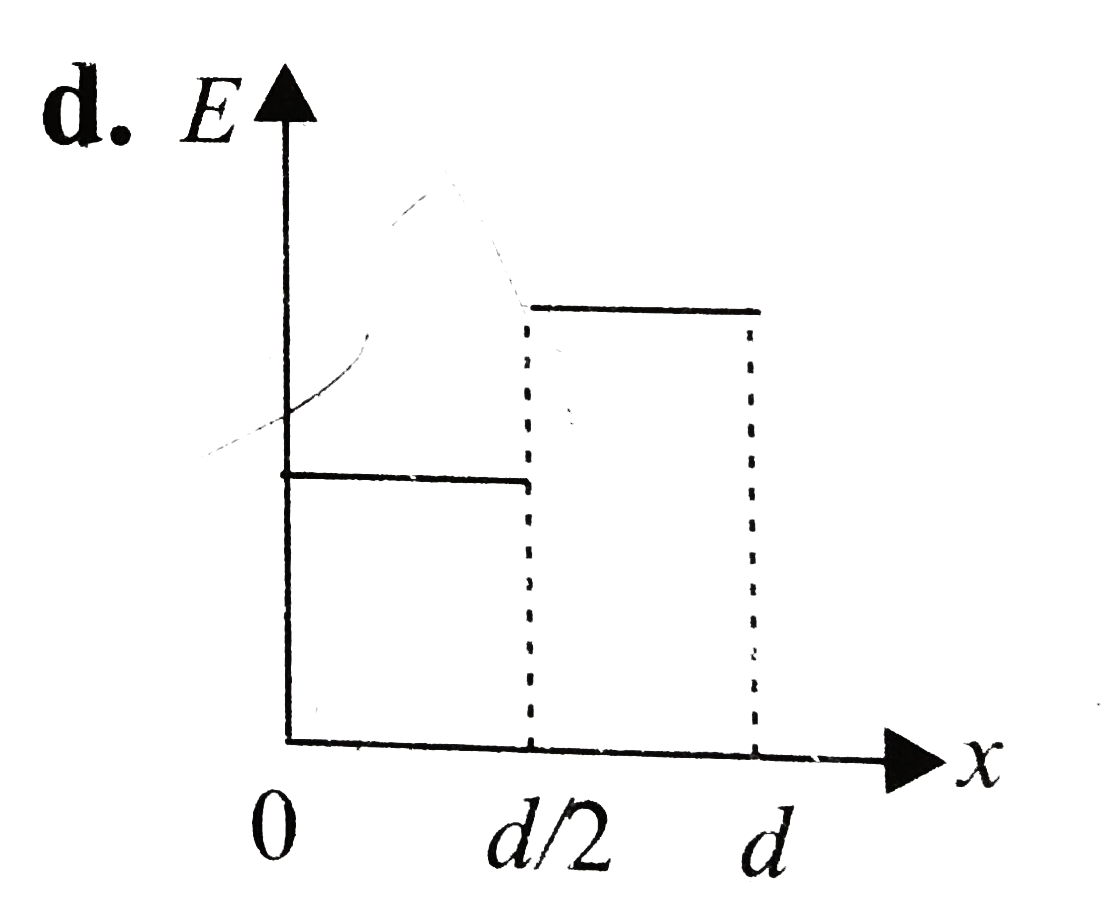
The space between the plates of a parallel plate air capacitor is filled with an isotropic dielectric medium of which dielectric constant varies in the direction perpendicular to the plates according to the relation given as
k=k1[1+sinπdx]
Where d is the separation, between the plates and k1 is a constant. The area of the plates is A. Determine the capacitance of the capacitor.
View SolutionThe gap between the plates of a plane capacitor is filled with an isotropic insulator whose di-electric constant varies in the direction perpendicular to the
plates according to the law K=K1[1+sin(π)dX] where d is the separation, between the plates & K1 is a constant. The area of the plates is S. Determine the capacitance of the capacitor.
View SolutionA parallel plate capacitor carries a harge Q. If a dielectric slab with dielectric constant K=2 is dipped between the plates, then
View SolutionHalf of the space between parallel plate capacitor is filled with a medium of dielectric constant K parallel to the plates . if initially the capacity is C, then the new capacity will be :
View SolutionThe space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical siza as shown in figure. If the dielectric constants of the three slabs are K1,K2andK3 find the new capacitance.

View Solution
