Define the collection {E1,E2,E3,.....} of ellipses and {R1,R2,R3,.....} of rectangles as follows:
E1=x29+y24=1 ,
R1 : rectangle of largest area, with sides parallel to the axes, inscribed in E1 ,
En : ellipse x2a2n+y2b2n=1 of largest are inscribed in Rn−1,n>1.
then which of the following options is/are corrct?
N∑n=1( area of Rn)<24, for each positive integer N
The distance of a focus from the centre in E9 is √532
The eccentricities of E18 and E19 are NOT equal
The length of latus rectum of E9 is 16
The correct Answer is:A, D
To solve the problem, we need to analyze the given ellipses and rectangles step by step. Let's break it down:
Step 1: Define the First Ellipse E1
The equation of the first ellipse is given as:
E1:x29+y24=1
From this equation, we can identify a2=9 and b2=4, which gives us:
- a=3
- b=2
Step 2: Find the Area of Rectangle R1
The rectangle R1 is inscribed in the ellipse E1 with its sides parallel to the axes. The vertices of the rectangle can be represented by the points (x,y) on the ellipse. The area A of the rectangle can be expressed as:
A=2x⋅2y=4xy
Using the parametric equations of the ellipse, we have:
x=3cosθandy=2sinθ
Substituting these into the area formula:
A=4(3cosθ)(2sinθ)=24cosθsinθ
Using the identity sin(2θ)=2sinθcosθ:
A=12sin(2θ)
Step 3: Maximize the Area of Rectangle R1
The maximum value of sin(2θ) is 1. Therefore, the maximum area of rectangle R1 is:
Amax=12⋅1=12
Step 4: Define the Subsequent Ellipses and Rectangles
For n>1, the ellipse En is inscribed in rectangle Rn−1. The dimensions of R1 are 6 (width) and 4 (height). The area of the rectangle Rn can be derived similarly, leading to:
Rn=2anbn
Where an and bn are the semi-major and semi-minor axes of the ellipse En.
Step 5: Generalize the Dimensions
The dimensions of the rectangles can be expressed as:
an=3√2n−1,bn=2√2n−1
Thus, the area of rectangle Rn becomes:
Rn=2⋅3√2n−1⋅2√2n−1=122n−1
Step 6: Calculate Total Area
The total area of all rectangles can be expressed as a geometric series:
Total Area=12(1+12+14+…)=12⋅11−12=12⋅2=24
Step 7: Analyze the Options
The options provided in the question likely relate to the areas calculated. Since the maximum area of the rectangles is 24, we can conclude that the area of each rectangle is less than or equal to 24.
Conclusion
Thus, the correct options based on the calculations are:
- The area of rectangles Rn is always less than 24.
- The values of E9 and E18 can be calculated similarly, leading to specific values.
The equation of the first ellipse is given as:
E1:x29+y24=1
From this equation, we can identify a2=9 and b2=4, which gives us:
- a=3
- b=2
The rectangle R1 is inscribed in the ellipse E1 with its sides parallel to the axes. The vertices of the rectangle can be represented by the points (x,y) on the ellipse. The area A of the rectangle can be expressed as:
A=2x⋅2y=4xy
Using the parametric equations of the ellipse, we have:
x=3cosθandy=2sinθ
Substituting these into the area formula:
A=4(3cosθ)(2sinθ)=24cosθsinθ
Using the identity sin(2θ)=2sinθcosθ:
A=12sin(2θ)
The maximum value of sin(2θ) is 1. Therefore, the maximum area of rectangle R1 is:
Amax=12⋅1=12
For n>1, the ellipse En is inscribed in rectangle Rn−1. The dimensions of R1 are 6 (width) and 4 (height). The area of the rectangle Rn can be derived similarly, leading to:
Rn=2anbn
Where an and bn are the semi-major and semi-minor axes of the ellipse En.
The dimensions of the rectangles can be expressed as:
an=3√2n−1,bn=2√2n−1
Thus, the area of rectangle Rn becomes:
Rn=2⋅3√2n−1⋅2√2n−1=122n−1
The total area of all rectangles can be expressed as a geometric series:
Total Area=12(1+12+14+…)=12⋅11−12=12⋅2=24
The options provided in the question likely relate to the areas calculated. Since the maximum area of the rectangles is 24, we can conclude that the area of each rectangle is less than or equal to 24.
Thus, the correct options based on the calculations are:
- The area of rectangles Rn is always less than 24.
- The values of E9 and E18 can be calculated similarly, leading to specific values.
Similar Questions
Two batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
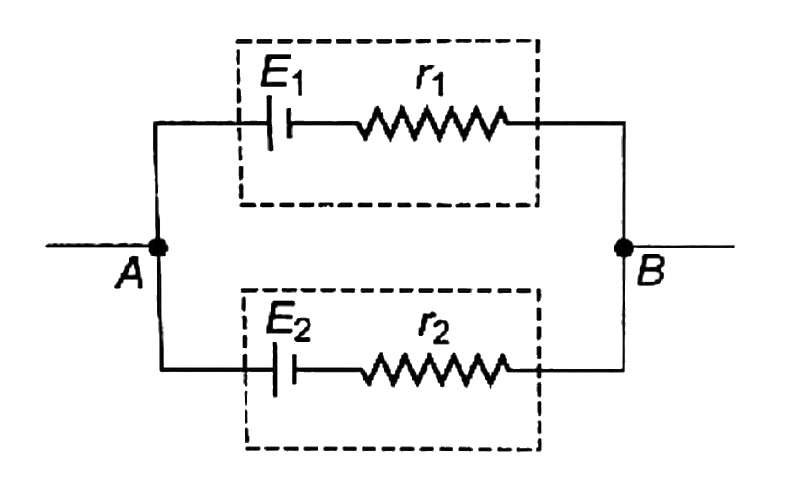 View Solution
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinates axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The length (in units) of the major axis of ellipse E2 is
View Solution
Knowledge Check
- Question 1 - Select One or More
Define the collections {E1,E2,E3,...} of ellipses and {R1,R2,R3,...} of rectangles as follows :
E1:x29+y24=1
R1: rectangle of largest area, with sides parallel to the axes, inscribed in E1,
Rn−1,n>1,
Rn : rectangle of largest area, with sides parallel to the axes, inscribed in En>1.
Then which of the following options is /are correct ?Athe eccentricities of E18 and E19 are NOT equal.BThe distance of a locus from the centre in E9is√532.CN∑n=1(area of Rn)<24, for each positive integer N.DThe length of latusrectum of E9is16. - Question 2 - Select One or More
For the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
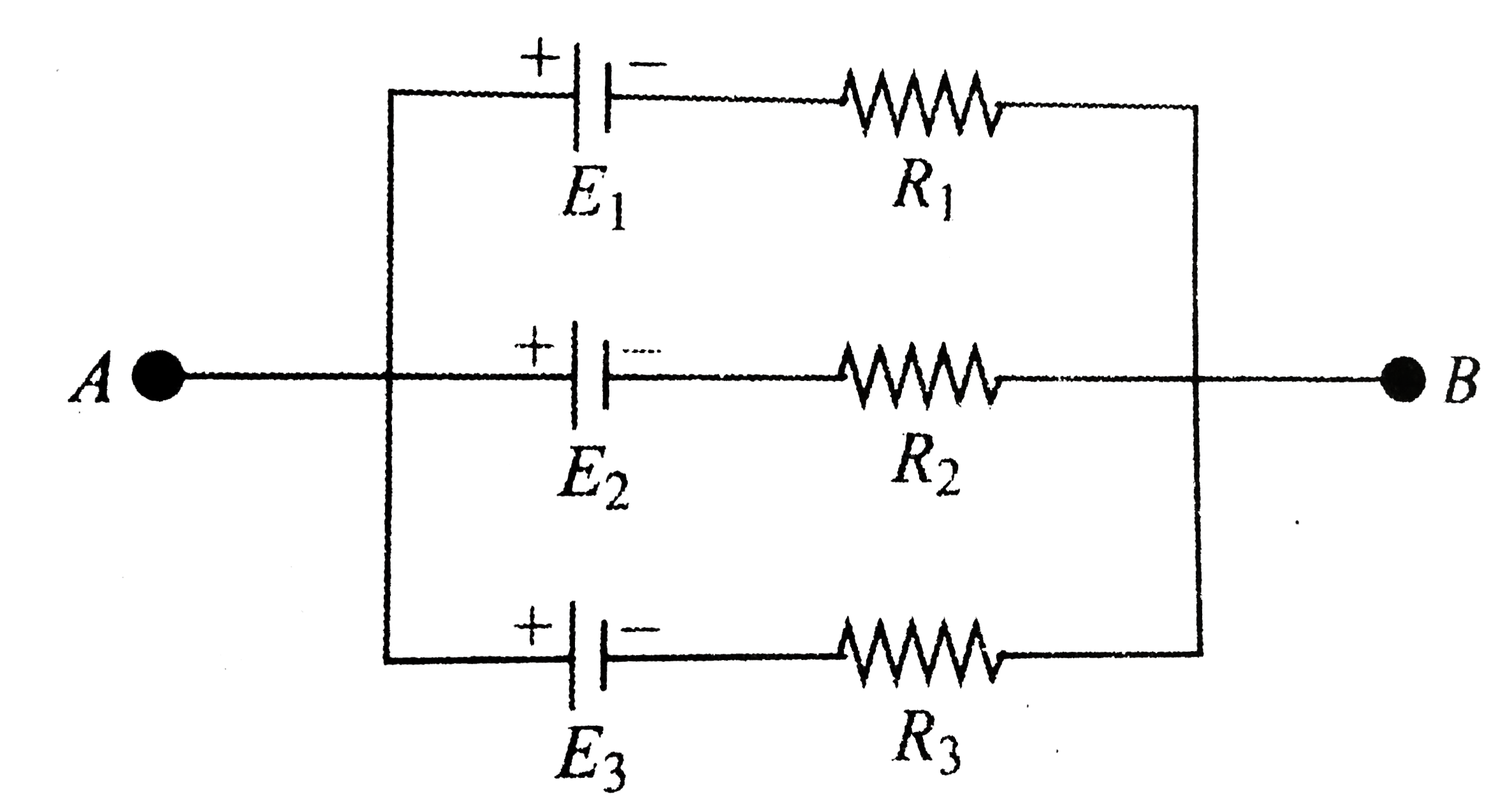 AThe equivalent internal resistance R of the system is given by (R1R2R3)/(R1R2+R2R3+R3R1).BIf E3=(E1R2+E2R1)/(R1+R2), the equivalent emf of the batteries will be equal to E3CThe equivalent emf to the battery is equal to E=(E1+E2+E3)/3DThe equivalent emf of the battery not only depends upon values of E1,E2,andE3 but also depends upon values of R1,R2andR3.
AThe equivalent internal resistance R of the system is given by (R1R2R3)/(R1R2+R2R3+R3R1).BIf E3=(E1R2+E2R1)/(R1+R2), the equivalent emf of the batteries will be equal to E3CThe equivalent emf to the battery is equal to E=(E1+E2+E3)/3DThe equivalent emf of the battery not only depends upon values of E1,E2,andE3 but also depends upon values of R1,R2andR3. - Question 3 - Select One or More
Equation of ellipse E1 is x29+y24=1, A rectangle R1, whose sides are parallel to co-ordinate axes is inscribed in E1 such that its area is maximum now En is an ellipse inside Rn−1 such that its axes is along co-ordinate axes and has maxmim possible area ∀n≥2,n∈N, further Rn is a rectangle whose sides are parallel to co-ordinate axes and is inscribed in En−1. Having maximum area ∀n≥2,n∈N
Am∑n=1 area of rectangle (Rn)<24∀m∈NBLength of latus rectum of E9=16CDistance between focus and centre of E9=√532DThe eccentricities of E18 and E19 are not equal.
The ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View SolutionIf e1 and e2 are respectively the eccentricities of the ellipse x218+y24=1 and the hyperbola x29−y24=1, then the relation between e1 and e2, is
View Solutionlet A1,A2,A3,...An are the vertices of a regular n sided polygon inscribed in a circle of radius R. If (A1A2)2+(A1A3)2+....(A1An)2=14R2 then find the number of sides in the polygon.
View SolutionIf (1+px+x2)n=1+a1x+a2x2+…+a2nx2n.
Which of the following is true for 1<r<2nView SolutionA series of concentric ellipse E1,E2,E3,…,En is constructed as follows: Ellipse En touches the extremities of the major axis of En−1 and have its focii at the extremities of the minor axis of En−1. If eccentricity of ellipse En is en, then the locus of (e2n,e2n−1) is
View Solution
