For the batteries shown in fig. R1,R2andR3 are the internal resistance of E1,E2,andE3, respectively Then, which of the following is / are correct?
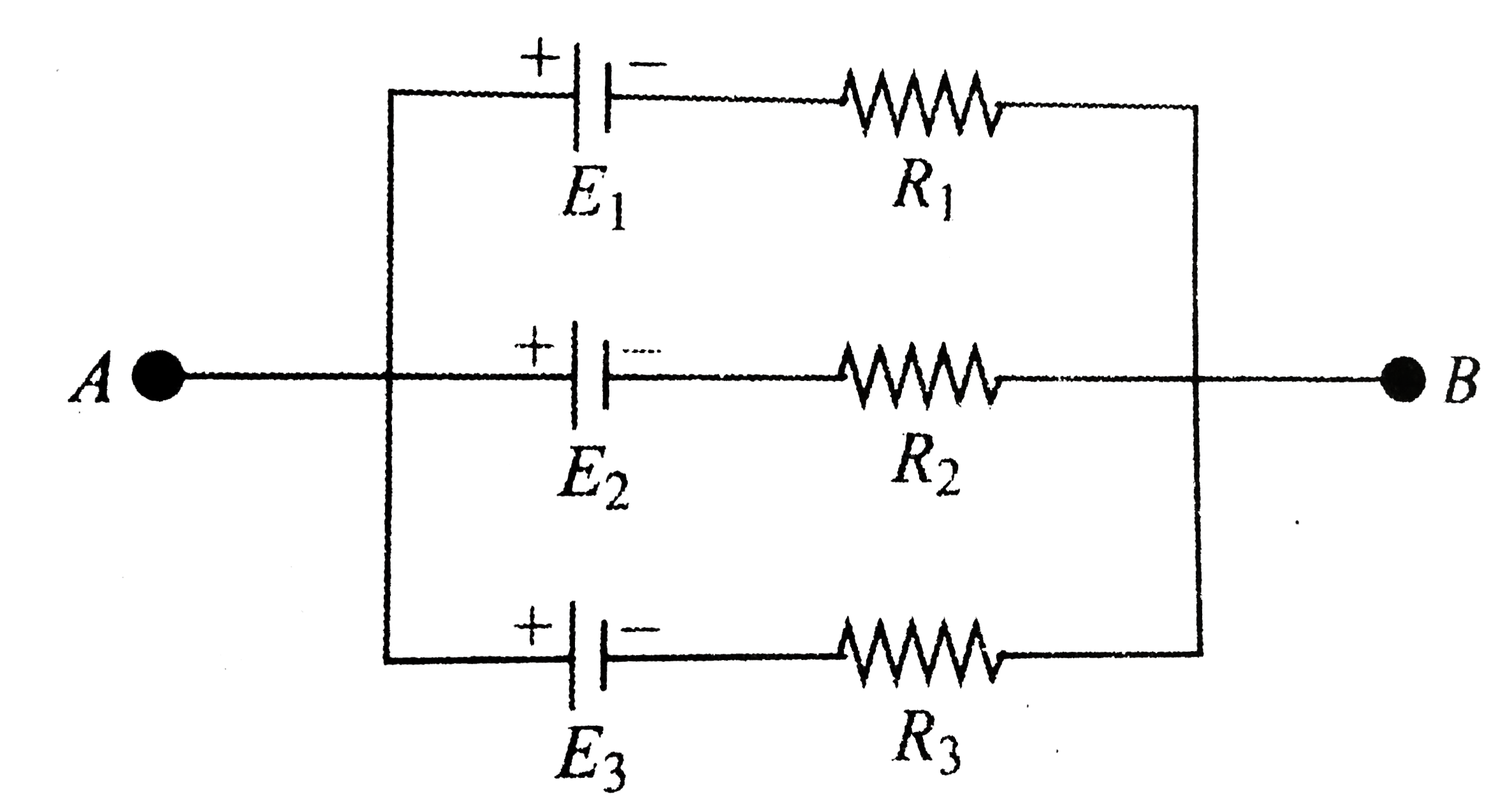
The equivalent internal resistance R of the system is given by (R1R2R3)/(R1R2+R2R3+R3R1).
If E3=(E1R2+E2R1)/(R1+R2), the equivalent emf of the batteries will be equal to E3
The equivalent emf to the battery is equal to E=(E1+E2+E3)/3
The equivalent emf of the battery not only depends upon values of E1,E2,andE3 but also depends upon values of R1,R2andR3.
The correct Answer is:A, B, D
We know that the equivalent internal resistance is
Req=1∑12=11R1+1R2+1R3
=R1R2R3R1R2+R2R+3+R3+R1
and the equivalent emf is
Eeq=∑ER∑1R=E1R1+E2R2+E3R31R1+1R2+1R3
Use E3=E1R2+E2R1R1+R2 to get
Eeq=E1R2+E2R1R1+R2=E3
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension35videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Single Correct72videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Find the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure
 View Solution
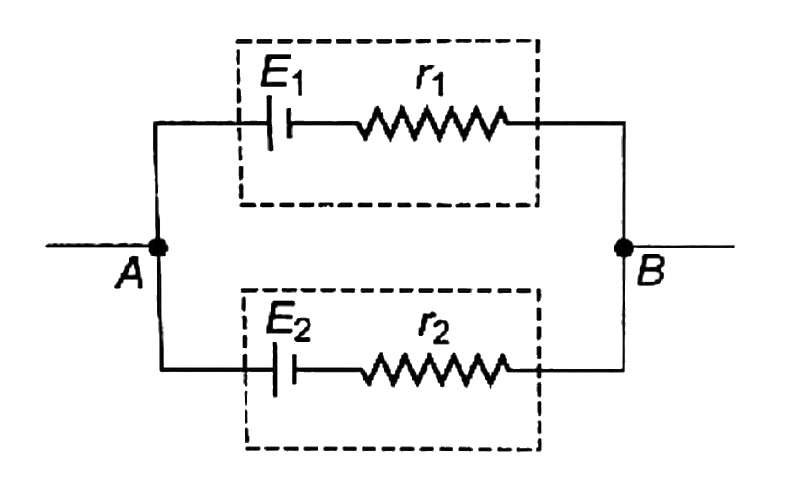
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A circuit consists of three batteries of emf E1 = 1 V, E2=2VandE3=3V and internal resistances 1Ω,2Ωand1Ω respectively which are connected in parallel as shown in the figure. The potential difference between points P and Q is
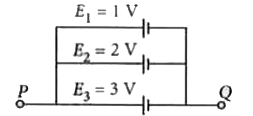 A1.0VB2.0VC2.2VD3.0V
A1.0VB2.0VC2.2VD3.0V - Question 2 - Select One
Two batteries of emf ε1 and ε2(ε2>ε1) and internal resistances r_1 and r2 respectively are connected in parallel as shown in Fig. Then
 Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2
Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2 - Question 3 - Select One
Three batteries of emf E1,E2 and E3 and internal resistance r1,r2 and r3 are connected as shown. The current through the battery of emf E3 is zero if.
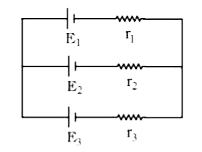 AE1r2+E2r1=E3(r1+r2)BE1r2−E2r1=E3(r1+r2)CE1r2+E2r1=E3(r1+r2)DE1r1+E2r2=E3(r1+r2)
AE1r2+E2r1=E3(r1+r2)BE1r2−E2r1=E3(r1+r2)CE1r2+E2r1=E3(r1+r2)DE1r1+E2r2=E3(r1+r2)
Find the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
 View Solution
View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View Solution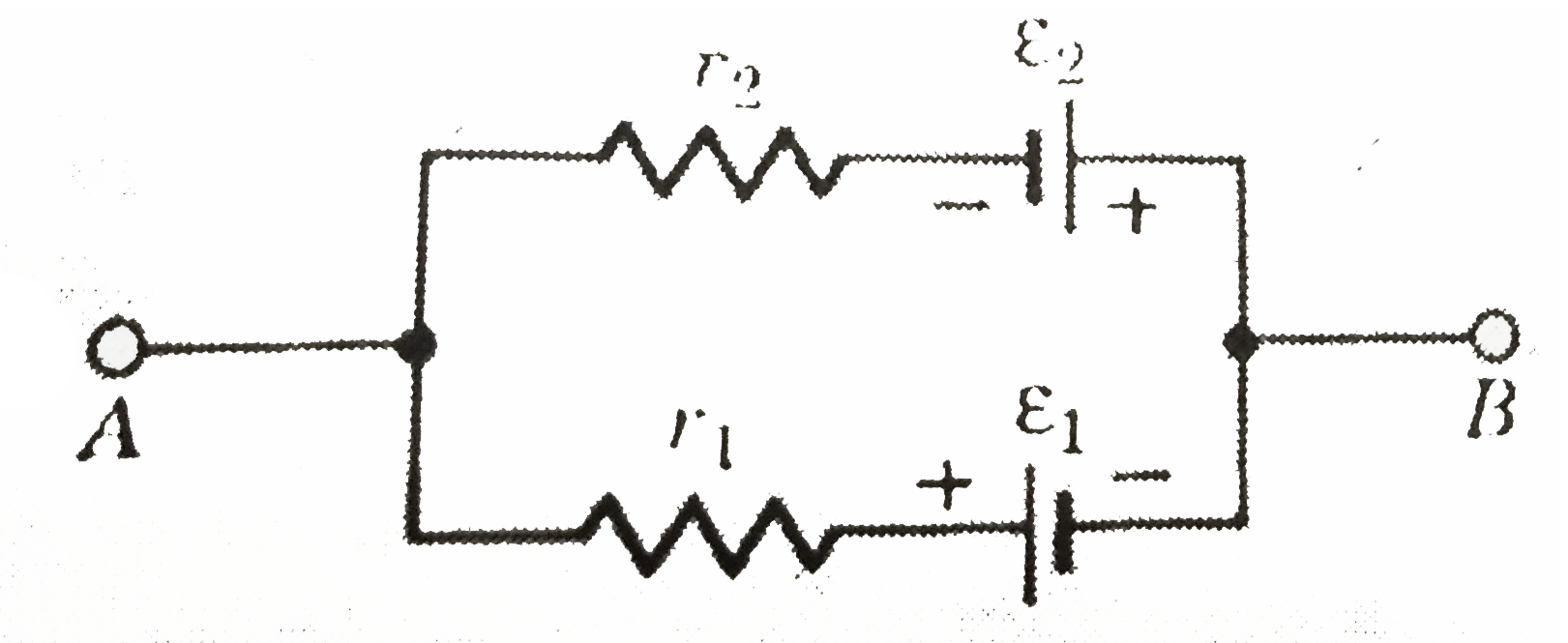
find the emf (ε0) and internal resistance (r0) if a battery which is equivalent to a parallel combination of two batteries of emfs ε1andε2 and internal resistances r1andr2 respectively, with polarities as shown in figure.View SolutionDefine the collections {E1,E2,E3,...} of ellipses and {R1,R2,R3,...} of rectangles as follows :
E1:x29+y24=1
R1: rectangle of largest area, with sides parallel to the axes, inscribed in E1,
Rn−1,n>1,
Rn : rectangle of largest area, with sides parallel to the axes, inscribed in En>1.
Then which of the following options is /are correct ?View SolutionTwo ideal batteries of emf V1andV2 and three resistances R1,R2andR3 are connected as shown in the figure. The current in resistance R2 would be zero if
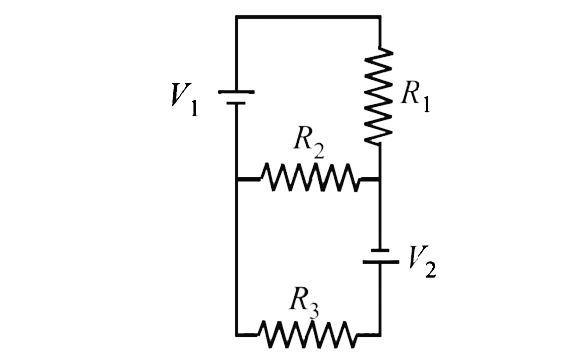 View Solution
View Solution

