Two discs of moments of inertia $I_{1} and I_{2}$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed $ω_{1} and ω_{2}$ are brought into contact face to face with their axes of rotation coincident . What is the angular speed of the two-disc system ?

Does the law of conservation of angular monentum apply to the situation ? Why ?

Find the angular speed of the two disc system .

Calculate the loss in kinetic energy of the system in the the process.

Account for this loss.

Video Solution

Text Solution

Verified by Experts

Consider the diagram below
let the common angular velocity of the system is $ω$
( A) yes , the law of conservation of angular momentum can be applied ,Because , there is no net external torque on the system of the two disc .
External forces , gravition and normal reaction ,act through th axis of rotation , hence produce no torque .

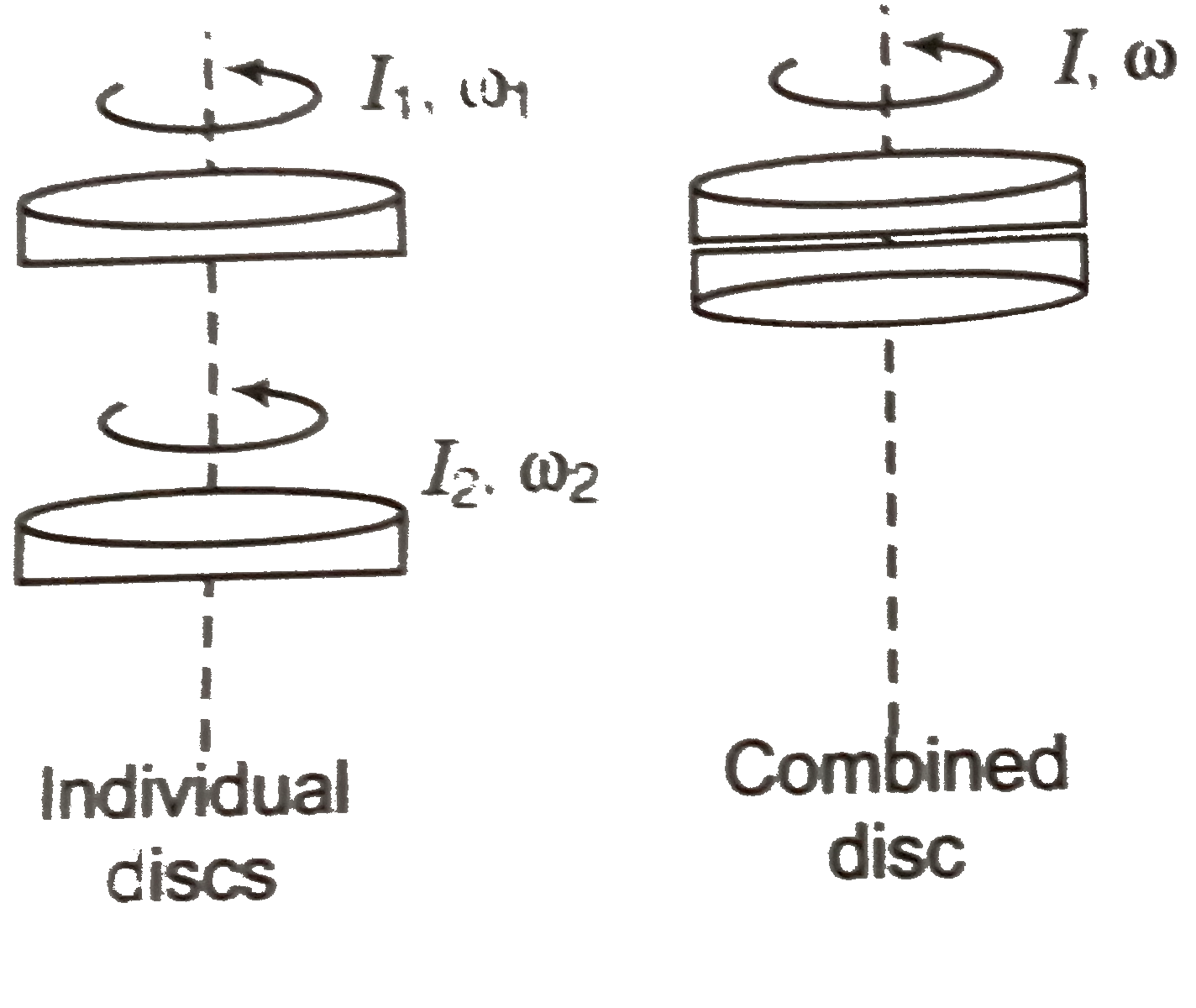
( B) BY conservation of angular momentum
$L_{f} = L_{j}$
$\Rightarrow I ω = I ω_{1} + I_{2} ω_{2}$
$\Rightarrow ω = \frac{I_{1} + I_{2} ω_{2}}{I} = \frac{I_{1} ω_{1} + I_{2} ω_{2}}{I_{1} + I_{2}} ⟨' I = I_{1} + I_{2})$
$(C) K_{f} = \frac{1}{2} (I_{1} + I_{2}) \frac{(I_{1} ω_{1} + I_{2} ω_{2})}{(I_{1} + I_{2})} = \frac{1}{2} \frac{(I_{1} ω_{1} + I_{2} ω_{2})}{(I_{1} + I_{2})}$
$k_{f} = \frac{1}{2} (I_{1} ω_{1}^{2} + I_{2} ω_{2}^{2})$
$Δ K = K_{f} - K_{i} = - \frac{I_{1} I_{2}}{2 (I_{1} + I_{2})} {(ω_{1} - ω_{2})}_{1}^{2} < 0$
(D) Hence there is loss in KE of the loss in kintic energy is mainly due to the work against the frication between the two discs.

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Two discs of moments of inertia $I_{1} and I_{2}$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds $ω_{1} and ω_{2}$ are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take $ω_{1} \neq ω_{2}$
ADoes the law of conservation of angular monentum apply to the situation ? Why ?
BFind the angular speed of the two disc system .
CCalculate the loss in kinetic energy of the system in the the process.
DAccount for this loss.
Question 2 - Select One
Two discs of moment of inertia $I_{1}$ and $I_{2}$ about their respectively axes (normal) to the disc and passing through the centre) , and rotating with angular speed $ω_{1}$ and $ω_{2}$ are brought into contact face to face with their axes of rotation coincident .
What is the loss in kinetic energy of the system in the process ?
A $\frac{I_{1} I_{2} {(ω_{1} - ω_{2})}_{1}^{2}}{2 (I_{1} + I_{2})}$
B $\frac{I_{1} I_{2} {(ω_{1} - ω_{2})}_{1}^{2}}{(I_{1} + I_{2})}$
C $\frac{I_{1} I_{2} {(ω_{1} + ω_{2})}_{1}^{2}}{(I_{1} - I_{2})}$
D $\frac{I_{1} I_{2} {(ω_{1} + ω_{2})}_{1}^{2}}{2 (I_{1} - I_{2})}$
Question 3 - Select One
Two discs of moments of inertia $I_{1}$ and $I_{2}$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed $ω_{1}$ and $ω_{2}$ are brought into contact face to face with their axes of rotation coincident. What is the loss in kinetic energy of the system in the process?
A $I_{1} I_{2} \frac{{(ω_{1} - ω_{2})}_{1}^{2}}{2} (I_{1} + I_{2})$
B $I_{1} I_{2} \frac{{(ω_{1} - ω_{2})}_{1}^{2}}{I_{1} + I_{2}}$
C $I_{1} I_{2} \frac{{(ω_{1} + ω_{2})}_{1}^{2}}{I_{1} - I_{2}}$
D $I_{1} I_{2} \frac{{(ω_{1} + ω_{2})}_{1}^{2}}{2} (I_{1} - I_{2})$

NCERT EXEMPLAR-SYSTEM OF PARTICLES AND ROTATIONAL MOTION -Long answer type questions

Home
Ask Doubt
Profile

Two discs of moments of inertia I1andI2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed ω1andω2 are brought into contact face to face with their axes of rotation coincident . What is the angular speed of the two-disc system ?

Topper's Solved these Questions

Similar Questions

Knowledge Check

NCERT EXEMPLAR-SYSTEM OF PARTICLES AND ROTATIONAL MOTION -Long answer type questions