A disc of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is μk.
(a) What was the velocity of its centre of mass before being brought in contact with the table ?
(b) What happens to the linear velocity of a point on its rim when placed in contact with the table ?
(c ) What happens to the linear speed of the centre of mass when disc is placed in contact with the table ?
(d) Which force i sresponsible for the effects in (b) and (c ).
(e) What condition should be satisfied for rolling to begin ?
(f) Calculate the time taken for the rolling to begin.
(a) Before being Brought in contact with the the was in in pure rotational motion hence vCM=0

(b) when the disc is placed in contact with the table due to friction velocity of a point on the rim decreases ,
(c) when the rotating disc is placed in correct with the table due to friction centre of mass acquiries some linear velocity .
friction is responsible for the effects in (b) and ( c)
(e) when rolling starts vCM−ωR.
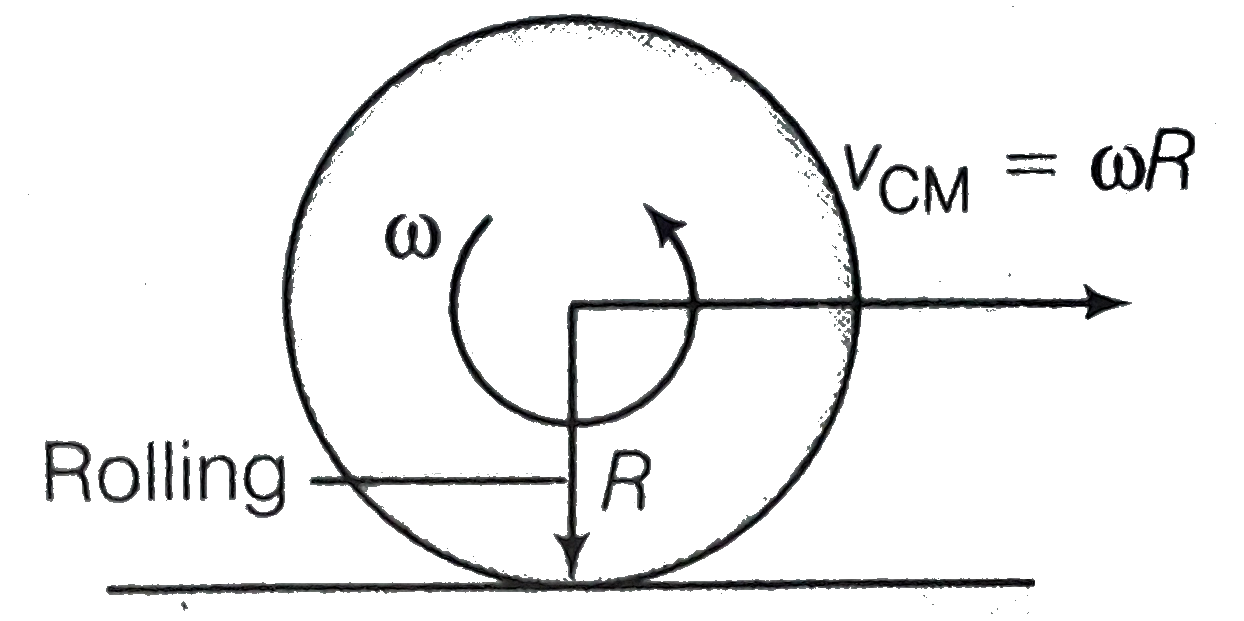
where ω is angular speed of the disc when rolling just starts.
(f) Acceleration produced in centre of mass due to friction
aCM=Fm=μkmgm=μkg.

Angular retardation produced by the torque due to fricton .
α=τI=μkmgRI [∵τ=(μkN)R=μkmgR]
∴vCM=uCM+aCMt
⇒VCM=μkgt(∵UCM=0)
andω=ω0+at
⇒ω=ω0−μkmgRIt
For rolling without sliping ,VCMR=ω
⇒VCMR=ω0−μkmgRIt
μkgtR=ω0−μkmgRIt
t=Rω0μkg(1+mR2I)
note in this problem , frictional force help in seting pure rolloing motion .
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLARCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - very short answer type questions
18 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLARCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - very short answer type questions
18 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLARCHAPTER - OSCILLATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
40 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLARCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
Similar Questions
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of a radius.
View Solution
Knowledge Check
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
Aω0μkR2gBω0g2μkRC2ω0RμkgDω0R2μkgA ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
Aω0μ1R2gBωaR2μgRC2ω0RωkgDω0R2μggA hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
Arω02Brω0Crω04Drω03
A disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View SolutionA disc rotating about its axis with angular speed ω0 is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A,BandC on the disc shown in Fig. Will the disc roll in the direction indicated ?
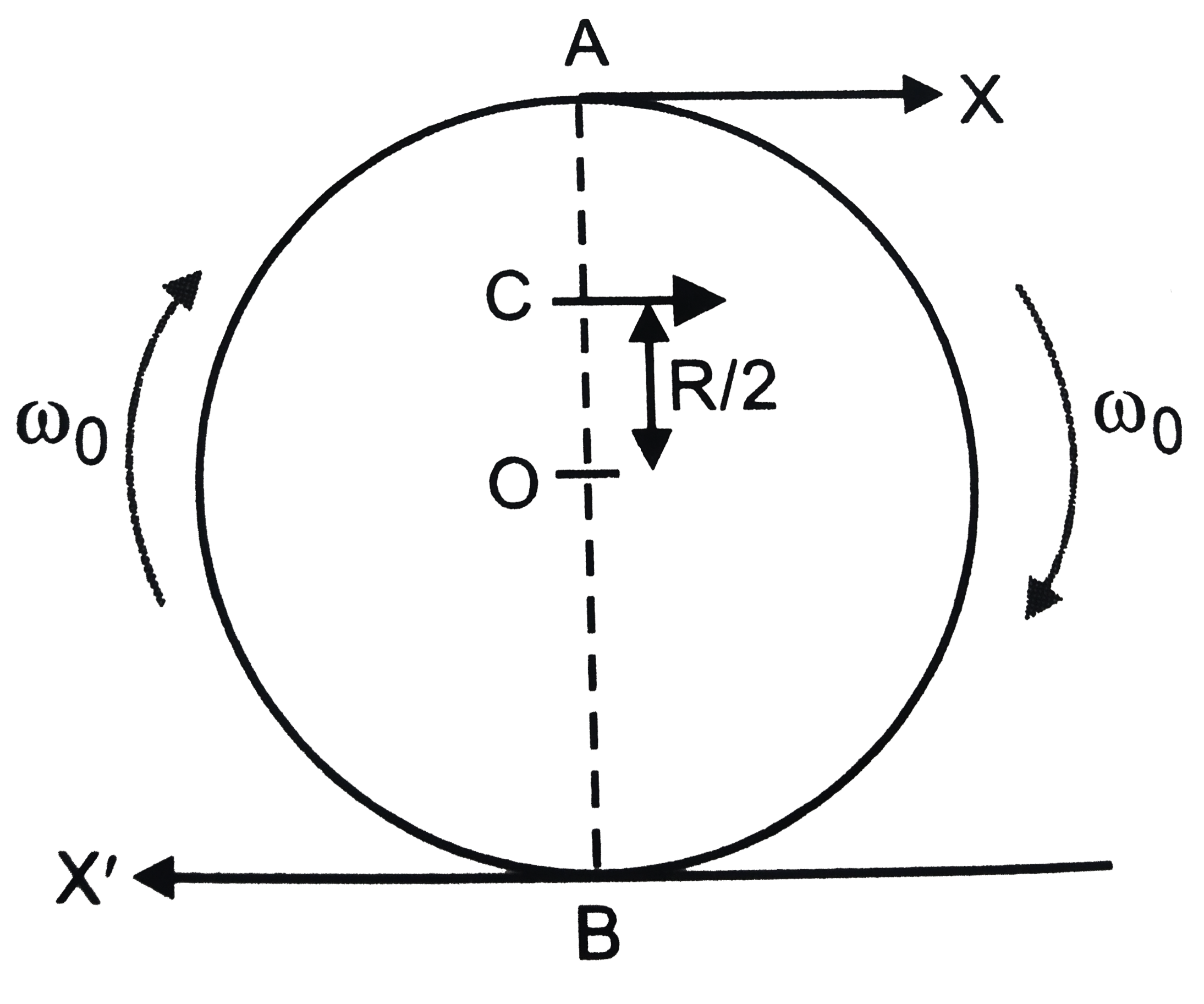
View SolutionA hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA disc is given an initial angular velocity ω0 and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are

View Solution
