In two right triangles, one side and an acute angle of one triangle are equal to one side and the corresponding acute angle of the other triangle. Prove that the two triangles are congruent.
Let ABC and DEF be two right triangles such that ∠A=∠D
and ∠B=∠E=900
BC=EF
Thus, in △ABCand △DEF, we have∠A=∠D(given)
∠B=∠E=900
and BC=EF
So, by AAS theorem we obtain△ABC≅△DEF
Topper's Solved these Questions
Similar Questions
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the other. Prove that the triangles are congruent.
Let ABC and DEF be two right triangles such that
∠A=∠D,BC=EFand∠B=∠E=900
Thus, in △s ABC and DEF<br>/_A=/_D<br>/_B=/_E=90^0<br>BC=EFSo,by∀S≅ruencecriterion,weobta∈<br>/_\ABC~=/_\DEFView SolutionIf hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent
View Solution
Knowledge Check
- Question 1 - Select One
If in two right triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent. 1.
PL is an altitude from P of ΔPQR on QR such that QL = LR. Then,A∠Q<∠RB∠Q=∠RC∠Q>∠RD∠P=∠R - Question 2 - Select One
If in two right triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent. 1.
In the figure, it is given that LM=MN,QM=MR,ML⊥PQandMN⊥PR. then
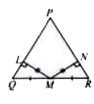 APQ<PRBPQ>PRCPQ=PRDNone of these
APQ<PRBPQ>PRCPQ=PRDNone of these
Which of the following statements are true and which of them are false?
(i) All squares are congruent.
(ii) If two squares have equal areas, they are congruent.
(iii) If two figures have equal areas, they are congruent.
(iv) If two triangles are equal in area, they are congruent.
(v) If two sides and one angle of a triangle are equal to the corresponding two sides and angle of another triangle, the triangles are congruent.
(vi) If two angles and any side of a triangle are equal to the corresponding angles and the side of another triangle then the triangles are congruent.
(vii) If three angles of a triangle are equal to the corresponding angles of another triangle then the triangles are congruent.
(viii) If the hypotenuse and an acute angle of a right triangle are equal to the hypotenuse and the corresponding acute angle of another right triangle then the triangles are congruent.
(ix) If the hypotenuse of a right triangle is equal to the hypotenuse of another right triangle then the triangles are congruent.View Solution
Prove that for a given correspondence, if three angles of one triangles are congruent to the corresponding three angles of the other triangle, then the two triangles are similar.View SolutionIf two sides and an angle of one triangle are equal to two sides and an angle of another triangle , then the two triangles must be congruent’. Is the statement true? Why?
View SolutionIf two sides and an angle of one triangle are equal to two sides and an angle of another triangle , then the two triangles must be congruent’. Is the statement true? Why?
View SolutionConsider the following statements : Two triangles are said to be congruent, if
1. Three angles of one triangle are equal to the corresponding three angles of the other triangle.
2. Three sides of one triangle are equal to the corresponding three sides of the other triangle,
3. Two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of the other triangle.
4. Two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle.
Which of the above statements are correct ?View SolutionIf in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle. Can you say that two triangles will be similar? Why?
View Solution

