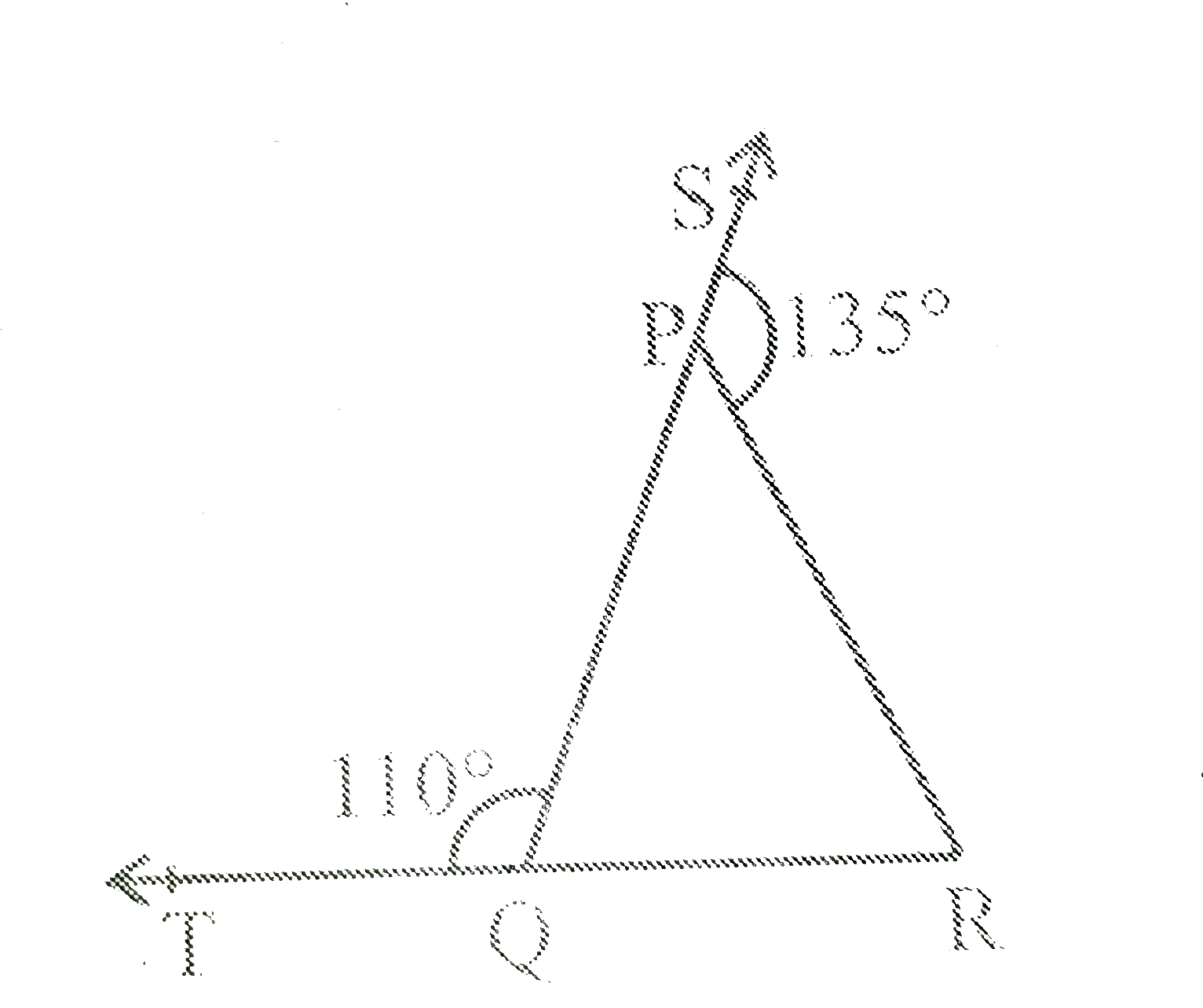
In figure, sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ. Figure
from figure ext∠SPR=∠PRQ+∠PQR
135∘=∠PRQ+∠PQR......(1)
∠PQT+∠PQR=180∘
110∘+∠PQR=180∘
∠PQR=70∘...(2)
from (1) and (2) we have
135∘=∠PRQ+70∘
∠PRQ=65∘
Topper's Solved these Questions
Similar Questions
In Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

View SolutionIn Figure, PQRS is a rhombus in which the diagonal PR is produced to T. If ∠SRT=1520, find x, y and z

View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.

View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.

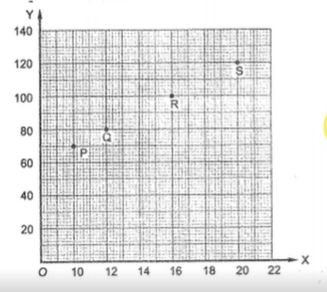
View SolutionFind the coordinates of points P, Q, R and S in Figure.
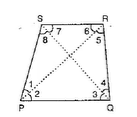
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
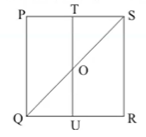
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
View Solution
