opp side of ||gm are ?
To prove that the opposite angles of a parallelogram are equal, we can follow these steps:
1. Define the Parallelogram:
Let’s consider a parallelogram ABCD, where AB is parallel to DC and AD is parallel to BC.
2. Identify the Transversal:
Take line AD as a transversal that intersects the parallel lines AB and DC.
3. Use the Property of Parallel Lines:
Since AB is parallel to DC, and AD is a transversal, we can state that:
∠A+∠D=180∘
(This is because the sum of the interior angles on the same side of the transversal is 180 degrees.)
4. Repeat for the Other Pair of Parallel Lines:
Now, consider line BC as a transversal that intersects the parallel lines AD and BC. Therefore, we can state that:
∠B+∠D=180∘
5. Set Up the Equations:
We now have two equations:
- Equation 1: ∠A+∠D=180∘
- Equation 2: ∠B+∠D=180∘
6. Subtract the Angles:
From both equations, we can set them equal to each other:
∠A+∠D=∠B+∠D
7. Cancel Out the Common Angle:
Subtract ∠D from both sides:
∠A=∠B
8. Prove the Other Pair of Opposite Angles:
Similarly, we can show that:
- By considering AD and BC as transversals, we can prove that:
∠C+∠D=180∘
and
∠A+∠C=180∘
Following the same steps as above, we can conclude that:
∠C=∠A
and
∠D=∠B
9. Conclusion:
Therefore, we have shown that:
∠A=∠Cand∠B=∠D
Hence, the opposite angles of a parallelogram are equal.
Let’s consider a parallelogram ABCD, where AB is parallel to DC and AD is parallel to BC.
Take line AD as a transversal that intersects the parallel lines AB and DC.
Since AB is parallel to DC, and AD is a transversal, we can state that:
∠A+∠D=180∘
(This is because the sum of the interior angles on the same side of the transversal is 180 degrees.)
Now, consider line BC as a transversal that intersects the parallel lines AD and BC. Therefore, we can state that:
∠B+∠D=180∘
We now have two equations:
- Equation 1: ∠A+∠D=180∘
- Equation 2: ∠B+∠D=180∘
From both equations, we can set them equal to each other:
∠A+∠D=∠B+∠D
Subtract ∠D from both sides:
∠A=∠B
Similarly, we can show that:
- By considering AD and BC as transversals, we can prove that:
∠C+∠D=180∘
and
∠A+∠C=180∘
Following the same steps as above, we can conclude that:
∠C=∠A
and
∠D=∠B
Therefore, we have shown that:
∠A=∠Cand∠B=∠D
Hence, the opposite angles of a parallelogram are equal.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Three statements are given below:
I. In a ||gm, the angle bisectors of two adjacent angles enclose a right angle.
I. The angle bisectors of a ||gm form a rectangle.
III. The triangle formed by joining the midpoints of the sides of an isosceles triangle is not necessarily an isosceles triangle.
Which is true?AI onlyBII onlyCI and IIDII and IIIIs ||gm ABCD a square?
I. Diagonals of ||gm ABCD are equal.
II. Diagonals of ||gm ABCD intersect at right angles.Aif the question can be answered by one of the given statements alone and not by the other,Bif the quesiton can be answered by either statement alone,Cif the question can be answered by both the statements together but not by any one of the two,Dif the question cannot be answered by using both the statements together.The area of ||gm ABCD is
 AAB×BMBBC×BNCDC×DLDAD×DL
AAB×BMBBC×BNCDC×DLDAD×DL
A 500gm liquid consist of 15gm ethane at any temp. T, at a pressure =2 atm. Find Pressure of gas required to dissolve 30gm gas in 300gm liquid.
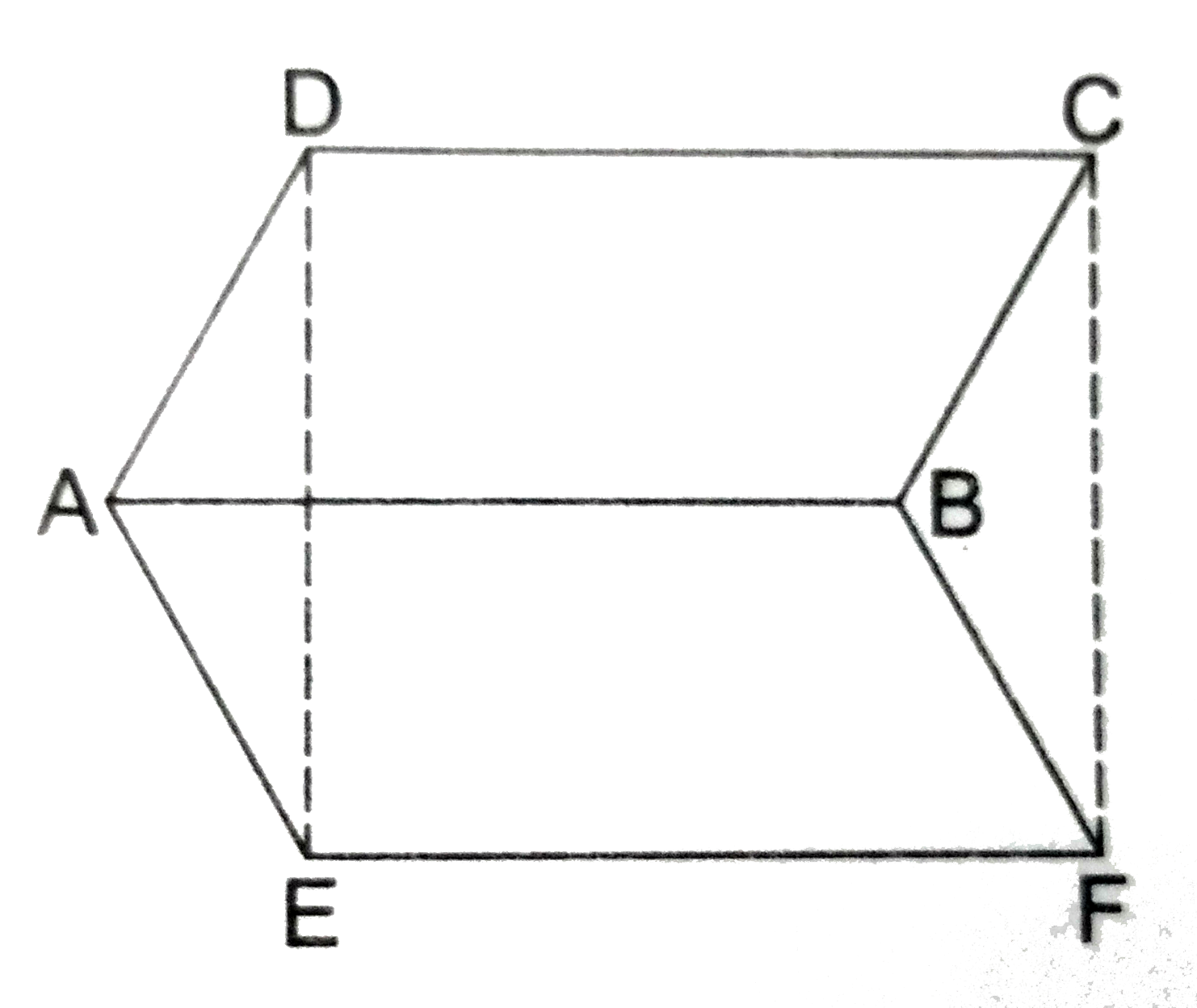
View SolutionThe side AB of a parallelogram ABCD is produced to any point E. A line through A and parallel to CE meets CB produced at G and then parallelogram EBGF is completed (see the figure). Prove that
area of ||gmABCD= area of ||gmBEFG.
View SolutionA wooden cube of side 10 cm and density 0.8 gm/cm3 is floating in water (density =1 gm/cm3). A mass of (100x) gm is placed over the cube so that cube is completely immersed without wetting the mass. Find value of x.
View SolutionOf al the ||gms of given sides: the ||gm which is rectangle has the greatest area
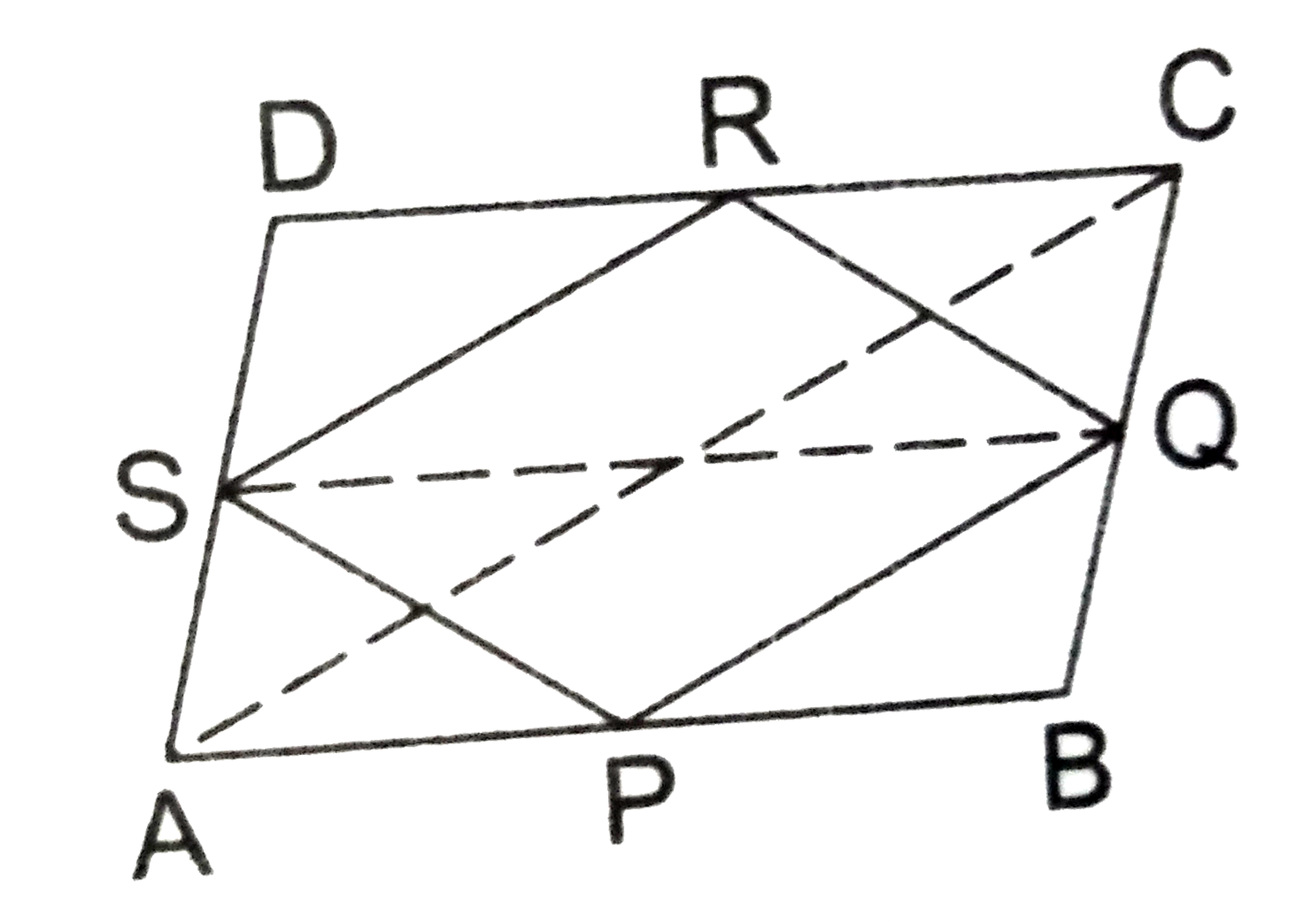
View SolutionP, Q, R, S are respectively the midpoints of the sides AB, BC, CD and DA of ||gm ABCD. Show that PQRS is a parallelogram and also show that
ar(|| gm PQRS)=12×ar(∣∣gmABCD).
View Solution