P, Q, R, S are respectively the midpoints of the sides AB, BC, CD and DA of ||gm ABCD. Show that PQRS is a parallelogram and also show that
ar(|| gm PQRS)=12×ar(∣∣gmABCD).
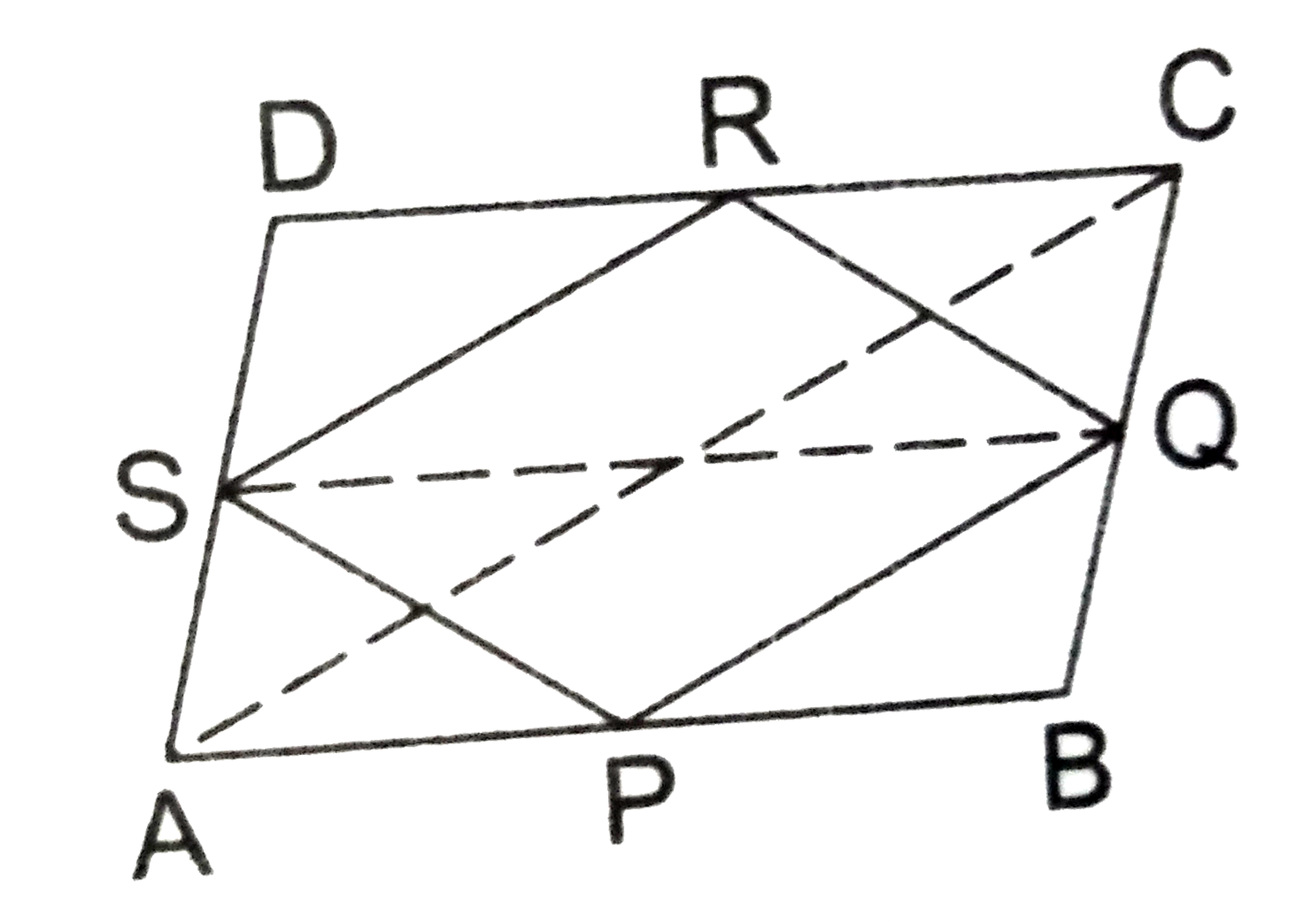
Step by step video, text & image solution for P, Q, R, S are respectively the midpoints of the sides AB, BC, CD and DA of ||gm ABCD. Show that PQRS is a parallelogram and also show that ar("|| gm PQRS")=(1)/(2)xxar("||gm ABCD). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
Let P, Q, R, S be respectively the midpoints of the sides AB, BC, CD and DA of quad. ABCD Show that PQRS is a parallelogram such that
ar(||gm PQRS)=12ar(quad. ABCD).
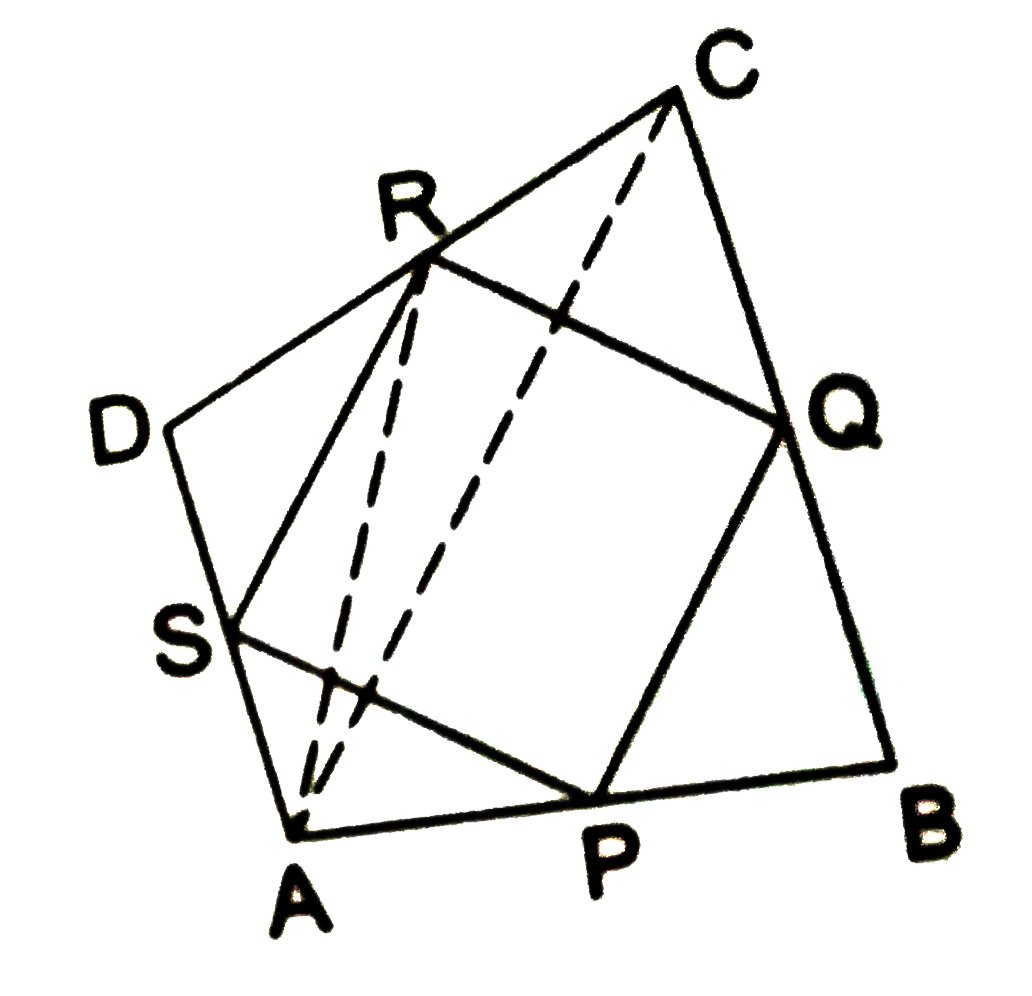 View Solution
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View Solution
Knowledge Check
- Question 1 - Select One
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
AACB12ACC23ACD32AC
P, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionABCD is a quadrilateral in which AB=CD and AD=BC. show that it is a parallelogram.
View SolutionIf E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=12ar(ABCD).
View SolutionIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, Show that ar(EFGH)=12AR (ABCD)
View SolutionThe quadrilateral formed by joining the mid-points of the sides AB, BC, CD, DA of a quadrilateral ABCD is
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View Solution

