The sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
Given: In parallelogram ABCD, E and F are the midpoints of the side AB and CD respectively.
DE and BF are joined.
To prove : EBFD is a parallelogram.
Construction: Join EF.
Proof :
∵ABCD is a parallelogram
∴AB = CD and AB || CD
(Opposite sides of a parallelogram are equal and parallel)
∴ EB || DF and EB = DF
(∵ E and F are mid points of AB and CD)
∴ EBFD is a parallelogram.
Topper's Solved these Questions
Similar Questions
The sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionIn a parallelogram ABCD , write the sum of angle A and B
View SolutionIn a ABC median AD is produced to X such that AD=DX . Prove that ABXC is a parallelogram.
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
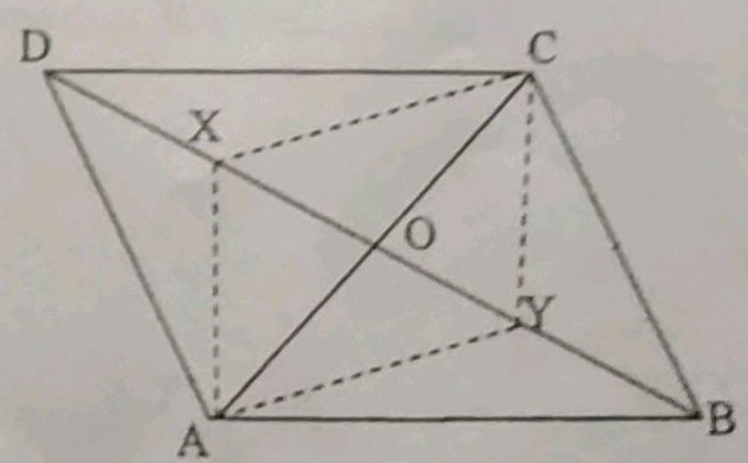
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
 View Solution
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
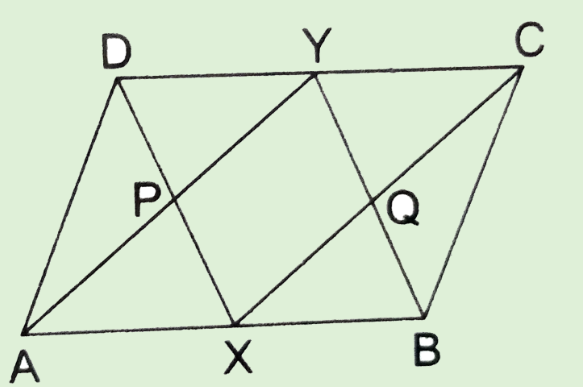
View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
 View Solution
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Find AB:AD
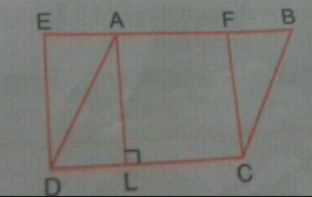
View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
 View Solution
View Solution

