The table shows the values of the quadratic functions f for several values of x. Which one of the following best represents f?
x−101 2f(x) 131−5
f(x)=−2x2
f(x)=x2+3
f(x)=−x2+3
f(x)=−2x2+3
The correct Answer is:D
To determine which quadratic function best represents the values given in the table, we will evaluate each option by substituting the values of x into the corresponding function and checking if the output matches the values of f(x).
Given Table:
- x:−1,0,1,2
- f(x):1,3,1,−5
Options to Check:
1. f(x)=−2x2
2. f(x)=3x+1
3. f(x)=−x2+3
4. f(x)=−2x2+3x
Step-by-Step Evaluation:
Step 1: Check Option 1: f(x)=−2x2
- For x=−1:
f(−1)=−2(−1)2=−2(not equal to 1)
- Since the output does not match, this option is incorrect.
Hint: Substitute x into the function and compare with the corresponding f(x).
Step 2: Check Option 2: f(x)=3x+1
- For x=−1:
f(−1)=3(−1)+1=−3+1=−2(not equal to 1)
- Since the output does not match, this option is incorrect.
Hint: Always check all given values of x for each option.
Step 3: Check Option 3: f(x)=−x2+3
- For x=−1:
f(−1)=−(−1)2+3=−1+3=2(not equal to 1)
- Since the output does not match, this option is incorrect.
Hint: Ensure to evaluate the function for all values of x given in the table.
Step 4: Check Option 4: f(x)=−2x2+3x
- For x=−1:
f(−1)=−2(−1)2+3(−1)=−2−3=−5(not equal to 1)
- For x=0:
f(0)=−2(0)2+3(0)=0(not equal to 3)
- For x=1:
f(1)=−2(1)2+3(1)=−2+3=1(equal to 1)
- For x=2:
f(2)=−2(2)2+3(2)=−8+6=−2(not equal to -5)
After checking all options, it seems none of the options perfectly match all the values in the table. However, the closest option that satisfies at least one point is option 4.
Conclusion:
None of the given options perfectly represent the function f based on the values provided in the table.
- x:−1,0,1,2
- f(x):1,3,1,−5
1. f(x)=−2x2
2. f(x)=3x+1
3. f(x)=−x2+3
4. f(x)=−2x2+3x
- For x=−1:
f(−1)=−2(−1)2=−2(not equal to 1)
- Since the output does not match, this option is incorrect.
- For x=−1:
f(−1)=3(−1)+1=−3+1=−2(not equal to 1)
- Since the output does not match, this option is incorrect.
- For x=−1:
f(−1)=−(−1)2+3=−1+3=2(not equal to 1)
- Since the output does not match, this option is incorrect.
- For x=−1:
f(−1)=−2(−1)2+3(−1)=−2−3=−5(not equal to 1)
- For x=0:
f(0)=−2(0)2+3(0)=0(not equal to 3)
- For x=1:
f(1)=−2(1)2+3(1)=−2+3=1(equal to 1)
- For x=2:
f(2)=−2(2)2+3(2)=−8+6=−2(not equal to -5)
None of the given options perfectly represent the function f based on the values provided in the table.
Similar Questions
Knowledge Check
- Question 1 - Select One
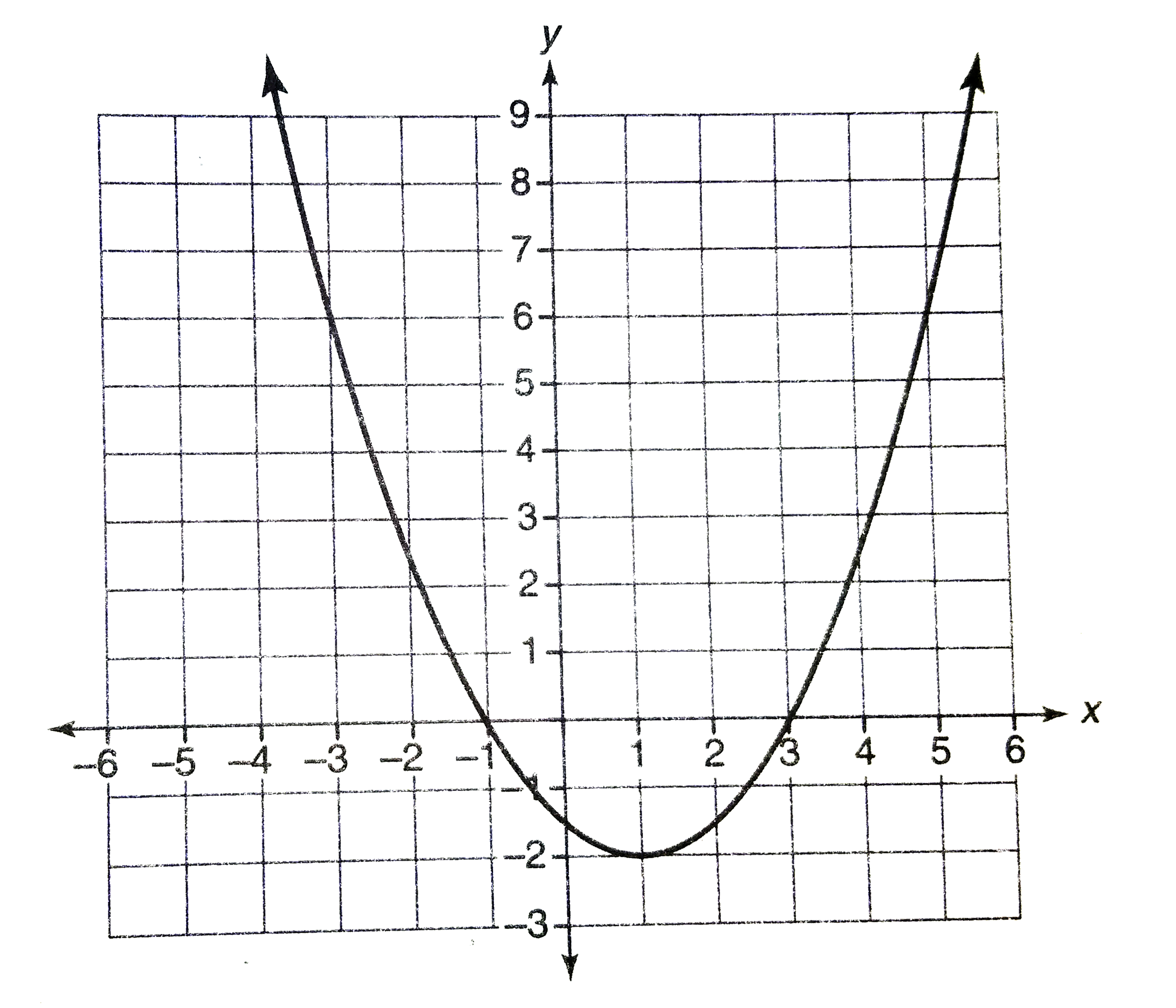
The figure above shows the graph of the quadratic function f with a minimum point at (1,−2). If f(5)=f(c), then which of the following could be the values of c?A−5B−3C0D6
The figure above shows the graph of function h. If function f is defined by f(x)=h(2x)+1, what is the value of f(−1)?
View SolutionLet f be a real valued function such that f(x)+3xf(1x)=2(x+1) for all real x>0. The value of f(5) is
View SolutionFind the values of x which the function f(x)=√log1/2(x−1x+5) is defined.
View SolutionThe maximum value of the function f(x) given by
f(x)=x(x−1)2,0<x<2 , isView Solutionif f(x)=x2sin(1x),x≠0 then the value of the function f at x=0 so that the function is continuous at x=0
View SolutionIf f(x)=x2+x+1, then find the value of 'x' for which f(x-1) =f(x)
View SolutionLet f,g:[−1,2]→R be continuous functions which are twice differentiable on the interval (-1, 2). Let the values of f and g at the points –1, 0 and 2 be as given in the following table : x=−1x=0x=2f(x)360g(x)01−1 In each of the intervals (-1,0) and (0, 2) the function (f – 3g)'' never vanishes. Then the correct statement(s) is(are)
View Solution

