Following are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one (s)

A

$v_{av} = \frac{1}{2} [v (t_{1}) + v (t_{2})]$

B

$v_{av} = \frac{r (t_{2}) - r (t_{1})}{t_{2} - t_{1}}$

C

$r = \frac{1}{2} (v (t_{2}) - v (t_{1})) (t_{2} - t_{1})$

D

$a_{av} = \frac{v (t_{2}) - v (t_{1})}{t_{2} - t_{1}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

If an object undergoes a displacement $Δ r$ in time $Δ t$ , its average velocity is given by
$v = \frac{Δ r}{Δ t} = \frac{r_{2} - r_{1}}{t_{2} - t_{1}}$ , where $r_{1}$ and $r_{2}$ are position vectors corresponding to time $t_{1}$ and $t_{2}$ .
It the velocity of an object changes from $v_{1}$ to $v_{2}$ in time $Δ t$ . Average acceleration is given by
$a_{a v} = \frac{Δ v}{Δ t} = \frac{v_{2} - v_{1}}{t_{2} - t_{2}}$
But , when acceleration is non-uniform
$v_{av} \neq \frac{v_{1} + v_{2}}{2}$
We can write $Δ v = \frac{Δ r}{Δ t}$
Hence, $Δ r = r_{2} - r_{1} = (v_{2} - v_{1}) (t_{2} - t_{1})$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Which of the following diagrams correctly relate displacement velocity and acceleration with time for a particle executing SHM
A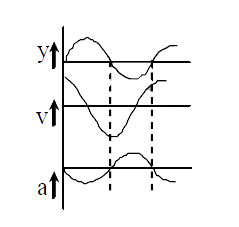
B
C
D
Question 2 - Select One
The diplacement , velocity and acceleration in a simple harmonic motion are related as the
Adisplacement , velocity and acceleration all act in the same directionb
Bdisplacement and velocity act in the same direction but acceleration in the opposite direction.
Cvelocity and acceleration are parallel and both are perpendicular to the displacement
Ddisplacement and acceleration are anti-parallel and both perpendicular to the velocity
Question 3 - Select One
The phase difference between displacement and acceleration of a particle in a simple harmonic motion is:
A $\frac{3 π}{2}$ rad
B $\frac{π}{2}$ rad
CZero
D $π$ rad

NCERT EXEMPLAR-MOTION IN A PLANE-Multiple Choice Questions

Home
Ask Doubt
Profile