A particle slides down a frictionless paraboli (y=x2) track (A−B−C) starting from rest at point A.Point B is at the vertex of parabola and point C is at a height less than that of point A.After C,the particle moves freely in air as a projectile. If the particle reaches highest point at P,then
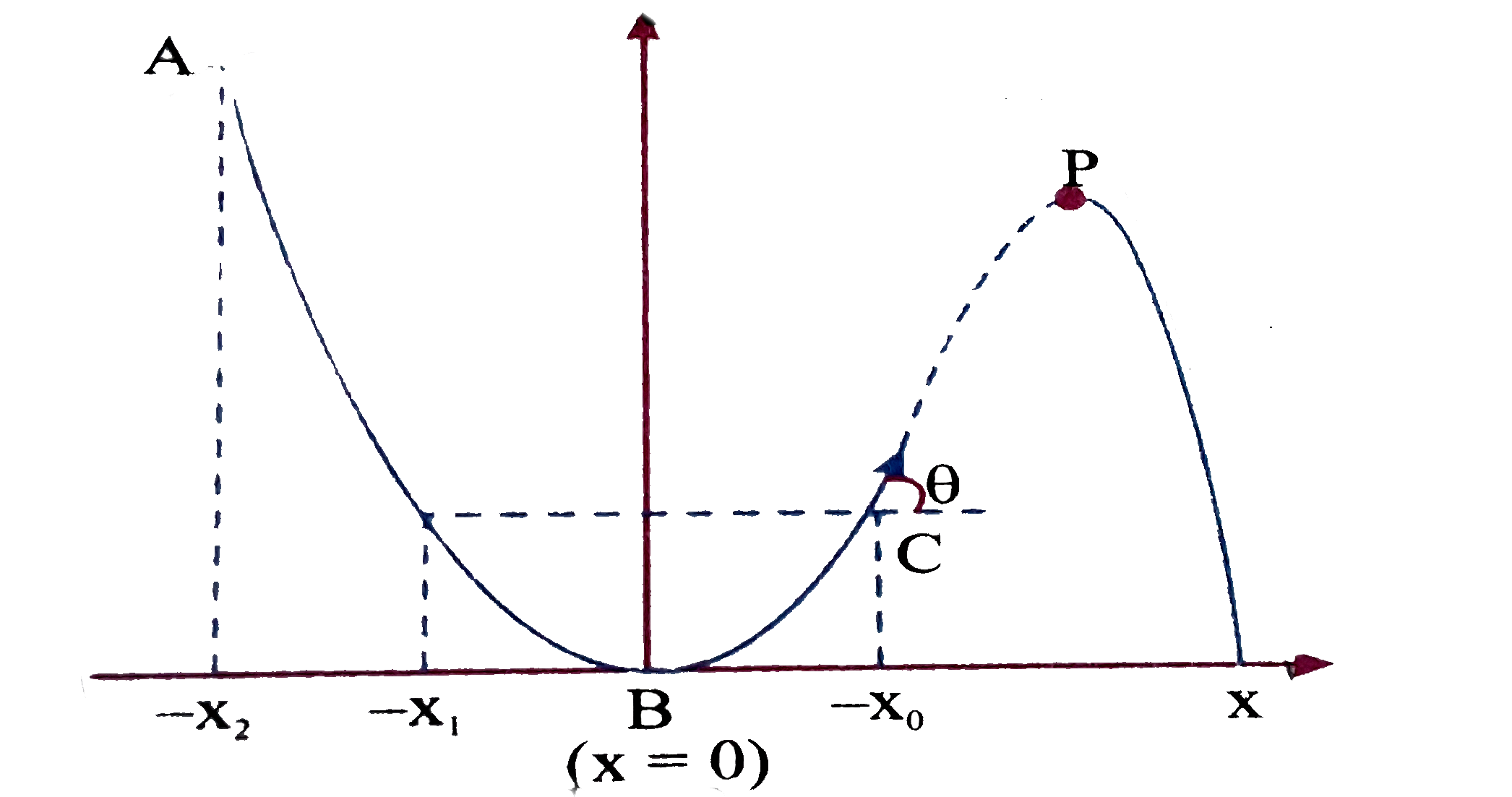
KE at P = KE at B
height at P=height at A
total energy at P= total energy at A
time of travel from A to B = time of travel from B to P
The correct Answer is:C
As the given track y=x2 is a frictionless track thus, total energy (KE + PE) will be same throughout the journey.
Hence, total energy at A = Total energy at P. At B, the particle is having only KE but at P some KE is converted to P.
Hence, (KE)B>(KE)P
Total energy at A = PE = Total energy at B =KE
Total energy at P
PE + KE
The potential energy at A, is converted to KE and PE at P, hence
(PE)P<(PE)A
Hence, (Height)P < (Height)A
As, height of P < Height of A
Hence, path length AB>path length BP
Hence, time of travel from A to B ≠ Time of travel from B to P.
Topper's Solved these Questions
Similar Questions
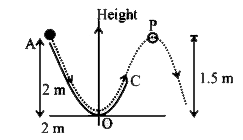
A particle (m = 3 kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaching its highest point P (height 1.5 m) the kinetic energy of the prarticle (in J) is : Figure drawn is schematic and not to scale , take g = 10ms−2
 View Solution
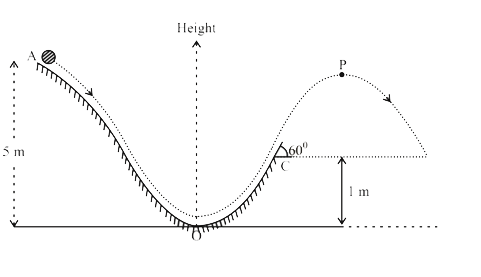
View SolutionA particle (m = 2 kg) slides down a smooth track AOC starting from rest at point A (height = 5m). After reaching point C (height =1m), the particle continues to move freely in air as a projectile. The particle velocity at point C is at angle 60∘ with the horizontal. The maximum height attained by particle after leaving point C is _____(in m). [figure drawn is schematic and hot to scale : take =ms−2]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m slides on a frictionaless surface ABCD, starting from rest as shown in figure. The part BCD is a circular arc. If it looses contact at point P, the maximum height attained by the particle from point C is
 A(a) R[2+12√2]B(b) R[1+12√2]RC(c) 3RD(d) None of these
A(a) R[2+12√2]B(b) R[1+12√2]RC(c) 3RD(d) None of these - Question 2 - Select One
Velocity of a particle varies with time as v=atˆi+2ht2ˆj. If the particle starts from point (0,c), the trajectory of the particle is
Ay=bx3/2a+cBy=4√2b3(xa)3/2+cCy=4√2b3(xa)3/2−cDy=bx3/2a−c - Question 3 - Select One
A particle starts from point A moves along a straight line path with an acceleration given by a=p−qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qp
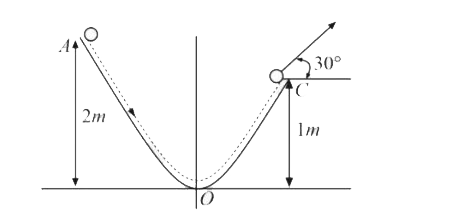
A particle (m = 1kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaches point C (height 1 m), the vertical speed of the particle (in m/s) is (Figure drawn is schematic and not to scale , take g = 9.8 m/sec2) [Take ]
 View Solution
View SolutionIn the illustration 1 if the particle shifts from Points P to points C find the displacement of the particle.
View Solution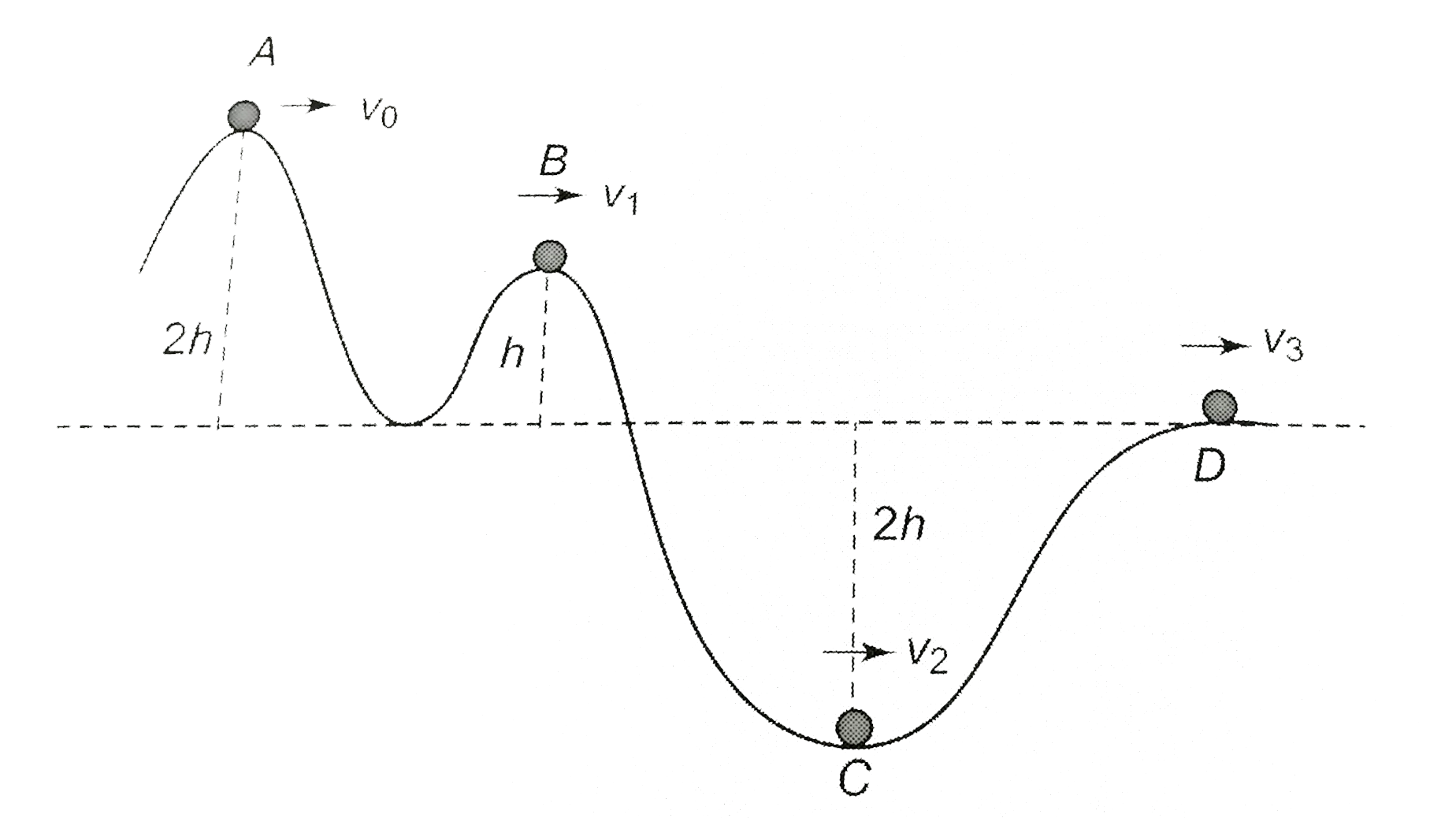
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and DView SolutionNormal to the parabola y2=8x at the point P (2, 4) meets the parabola again at the point Q. If C is the centre of the circle described on PQ as diameter then the coordinates of the image of point C in the line y=x are
View SolutionA particle moves on a path as shown. The particle takes 10 seconds in going from starting point to the final point. What is the average velocity vector of the particle ?
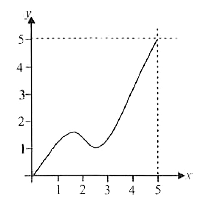 View Solution
View Solution

