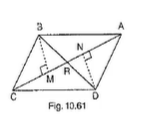
In a ABC, BM and CN are perpendiculars from B and C respectively on any line passing through A. If L is the mid-point of BC , prove that ML=NL.
Construction: Draw OL perpendicular to MN.
Now, If a transversal makes equal intercepts on three or more parallel lines, then any other transversal intersecting them will also make equal intercepts.
BM, CN and OL are perpendicular to MN
Therefore, BM parallel to CN parallel to OL.
Now, BM parallel to CN parallel to OL and BC is the transversal making equal intercepts
i.e. BL=LC
Therefore, transversal MN willl also make equal intercepts.
OM=ON
In triangles LMO and LNO,
OM=ON
∠LOM=∠LON=90∘
OL is common
As both triangles are congruent.
∴LM=LN(CPCT)
Hence Proved.
Topper's Solved these Questions
Similar Questions
BM and CN are perpendicular to a line passing through the vertex A of a triangle ABC. If L is the mid-point of BC , prove that LM=LN
View SolutionBD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LCM)=ar(LBM)
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)
View SolutionIn a ABC , If LandM are points on ABandAC respectively such that LMparallel BC
Prove that: ar(LOB)=ar(MOC)
View SolutionIn a ABC , If LandM are points ABandAC respectively such that LMparallelBC
Prove that: ar(ABM)=ar(ACL)
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn ABC , AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O , prove that: (i) OMAOLC (ii) OAOC=OMOL
View SolutionIn Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
View Solution