Prove that If the medians of a ABC
intersect at G,
show that
ar(AGB)=ar(AGC)=ar(BGC)=13ar(ABC)
In∠ABC, AD is median
ar(∠ABD)=ar(∠ACD)−(1)
In∠GBC,GD is median
ar(∠GBD)=ar(∠GCD)−(2)
subtracting equation 2 from 1
ar(∠ABG)=ar(∠ACG)−(3)
ar(∠AGB)=ar(∠BGC)−(4)
ar(∠ABG)=ar(∠BGC)=ar(∠ACC1)
ar(∠ABG)+ar(∠ABG)+ar(∠ABG)=ar(∠ABC)
ar(ABG)=13ar(∠ABC).
Topper's Solved these Questions
Similar Questions
Prove that If the medians of a ABC intersect at G, show that ar(AGB)=ar(AGC)=ar(BGC)=13ar(ABC)
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area. GIVEN : A parallelogram ABCD . The diagonals AC and BD intersect at O. TO PROVE : ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that : ar(ADEG)=ar(GBCE) ar(EGB)=16ar(ABCD)
View SolutionIf AD is median of ABC and P is a point on AC such that ar (ADP): ar (ABD)=2:3, then ar(PDC):ar (ABC) is 1:5 (b) 1:5 (c) 1:6 (d) 3:5
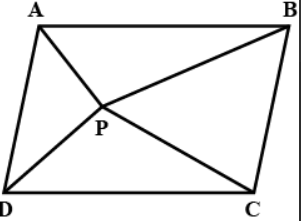
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
 View Solution
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionThe medians BE and CF of a triangle ABC intersect at G. Prove that area of GBC=area of quadrilateral AFGE.
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
 View Solution
View SolutionMedians of ABC intersect at G . If ar (ABC)=27 cm2, then ar (ABGC)= 6 cm2 (b) 9 cm2 (c) 12 cm2 (d) 18cm2
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View Solution

