In the figure given below, the area of the shaded region is $44 c m^{2}$ . O is the centre of the semi-circle, $¯ ¯¯¯¯ ¯ O E ⊥ ¯ ¯¯¯¯ ¯ O D$ and $¯ ¯¯¯¯ ¯ O C ⊥ ¯ ¯¯¯¯ ¯ A B$ . The area of the region POQR (in $c m^{2}$ ) if $O E = 7 c m$ is

Video Solution

Answer

Step by step video & image solution for In the figure given below, the area of the shaded region is 44 cm^2. O is the centre of the semi-circle, bar(OE) _|_ bar(OD) and bar(OC) _|_ bar(AB). The area of the region POQR (in cm^2) if OE=7cm is by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS QUESTION BANK

Similar Questions

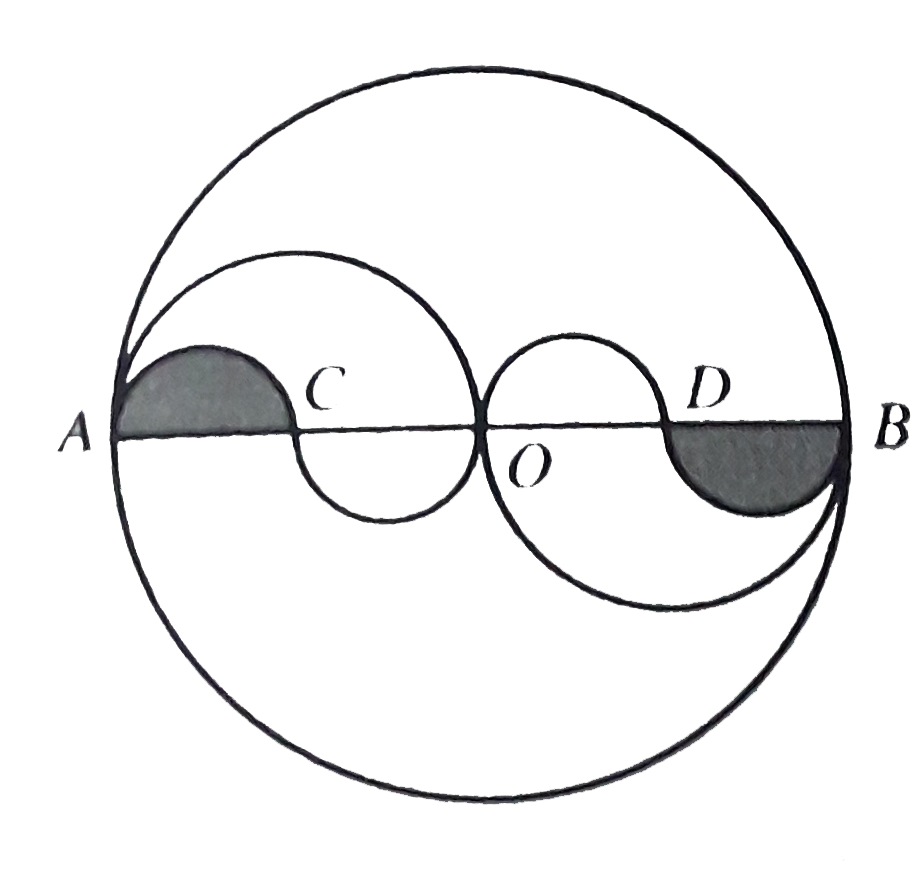
In the circle shown above, O is the center and $¯ ¯¯¯¯ ¯ A B$ is a diameter . There are two semicircles with diameters $¯ ¯¯¯¯ ¯ A O$ and $¯ ¯¯¯¯ ¯ B O$ , and four smaller semicircles with congruent diameters $¯ ¯¯¯¯ ¯ A C, ¯ ¯¯¯¯ ¯ C O, ¯ ¯¯¯¯ ¯ O D$ and $¯ ¯¯¯¯ ¯ D B$ . A point is picked at random in the large circle . What is the probability that it lands in a shaded region ?
View Solution
In Fig, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
shaded region.
View Solution
In the figure, O is the centre of the circle and AB = CD. OM is perpendicular on $¯ ¯¯¯¯ ¯ A B$ and $¯ ¯¯¯¯ ¯ O N$ is perpendicular on $¯ ¯¯¯¯ ¯ C D$ . Then prove that OM = ON.

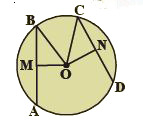
View Solution
In the figure, O is the centre of the circle and AB = CD. OM is perpendicular on bar(AB) and bar(ON) is perpendicular on bar(CD) . Then prove that OM = ON.
View Solution
In the figure, O is the centre of the circle and AB = CD. OM is perpendicular on $¯ ¯¯¯¯ ¯ A B$ and $¯ ¯¯¯¯ ¯ O N$ is perpendicular on $¯ ¯¯¯¯ ¯ C D$ . Then prove that OM = ON.

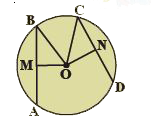
View Solution
In the figure, O is the centre of the circle and AB = CD. OM is perpendicular on $¯ ¯¯¯¯ ¯ A B$ and $¯ ¯¯¯¯ ¯ O N$ is perpendicular on $¯ ¯¯¯¯ ¯ C D$ . Then prove that OM = ON.

View Solution
If OABC, OCDE, OEFA are adjacent faces of a cube OABCDEF then $¯ ¯¯¯¯ ¯ O B + ¯ ¯¯¯¯ ¯ O D + ¯ ¯¯¯¯ ¯ O F$ interms of $¯ ¯¯¯¯ ¯ O A, ¯ ¯¯¯¯ ¯ O E, ¯ ¯¯¯¯ ¯ O C$ is
View Solution
If D, E, F are mid points of sides BC, CA, AB of triangle ABC and G is centroid then
$\begin{matrix} List-I & List-II A) ¯ ¯¯¯¯ ¯ A D + ¯ ¯¯¯¯ ¯ B E + ¯ ¯¯¯¯ ¯ C F & 1) ¯ ¯¯¯¯ ¯ C B B) ¯ ¯¯¯¯ ¯ G A + ¯ ¯¯¯¯ ¯ G B & 2) 3 ¯ ¯¯¯¯ ¯ O G C) ¯ ¯¯¯¯ ¯ A B + ¯ ¯¯¯¯ ¯ C A & 3) ¯ ¯ ¯ O D) ¯ ¯¯¯¯ ¯ O D + ¯ ¯¯¯¯ ¯ O E + ¯ ¯¯¯¯ ¯ O F & 4) - \frac{2}{3} (¯ ¯¯¯¯ ¯ A D + ¯ ¯¯¯¯ ¯ B E) 5) 3 ¯ ¯¯¯ ¯ O I \end{matrix}$
The correct matching is
View Solution

In the figure given below, the area of the shaded region is 44cm2. O is the centre of the semi-circle, ¯¯¯¯¯¯OE⊥¯¯¯¯¯¯OD and ¯¯¯¯¯¯OC⊥¯¯¯¯¯¯AB. The area of the region POQR (in cm2) if OE=7cm is

Similar Questions

Recommended Questions

In the figure given below, the area of the shaded region is $44 c m^{2}$ . O is the centre of the semi-circle, $¯ ¯¯¯¯ ¯ O E ⊥ ¯ ¯¯¯¯ ¯ O D$ and $¯ ¯¯¯¯ ¯ O C ⊥ ¯ ¯¯¯¯ ¯ A B$ . The area of the region POQR (in $c m^{2}$ ) if $O E = 7 c m$ is