The graph of the function y = g(x) is shown. The number of solutions of the equationm ||g(x)|−1|=12, is
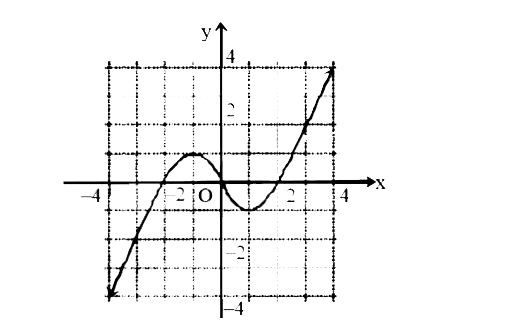
4
5
6
8
The correct Answer is:D
Step by step video, text & image solution for The graph of the function y = g(x) is shown. The number of solutions of the equationm abs(absg(x)-1)=1/2, is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FUNCTIONBOOK - MOTIONCHAPTER - FUNCTIONEXERCISE - Exercise - 2 (Level-I)
33 Videos
- FUNCTIONBOOK - MOTIONCHAPTER - FUNCTIONEXERCISE - Exercise - 2 (Level-II)
6 Videos
- FUNCTIONBOOK - MOTIONCHAPTER - FUNCTIONEXERCISE - Exercise - 4 | Level-II
7 Videos
- ELLIPSE BOOK - MOTIONCHAPTER - ELLIPSE EXERCISE - Exercise - 4 | Level-I Previous Year | JEE Main
20 Videos
- HYPERBOLABOOK - MOTIONCHAPTER - HYPERBOLAEXERCISE - EXERCISE-4 (Level-II)
17 Videos
Similar Questions
Knowledge Check
The graph of y = f(x} is shown, then the number of solutions of f(f(x}} = 2 will be
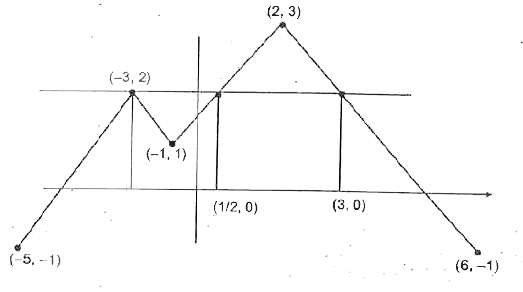 A1B2C3D4
A1B2C3D4If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isA B
B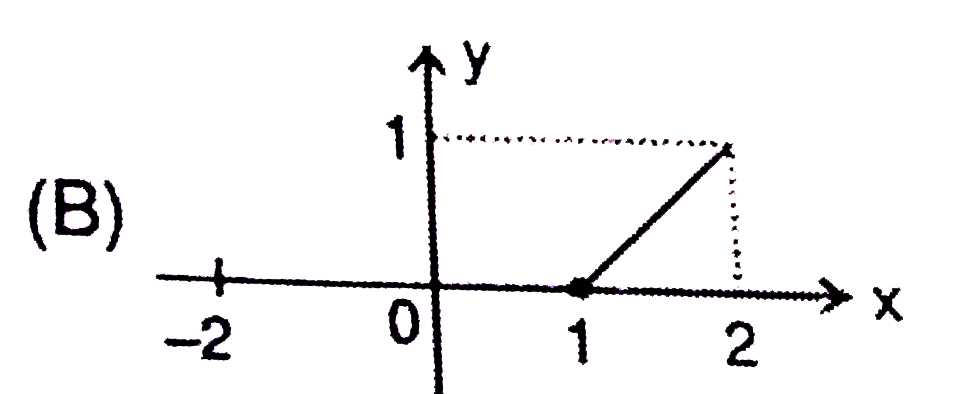 C
C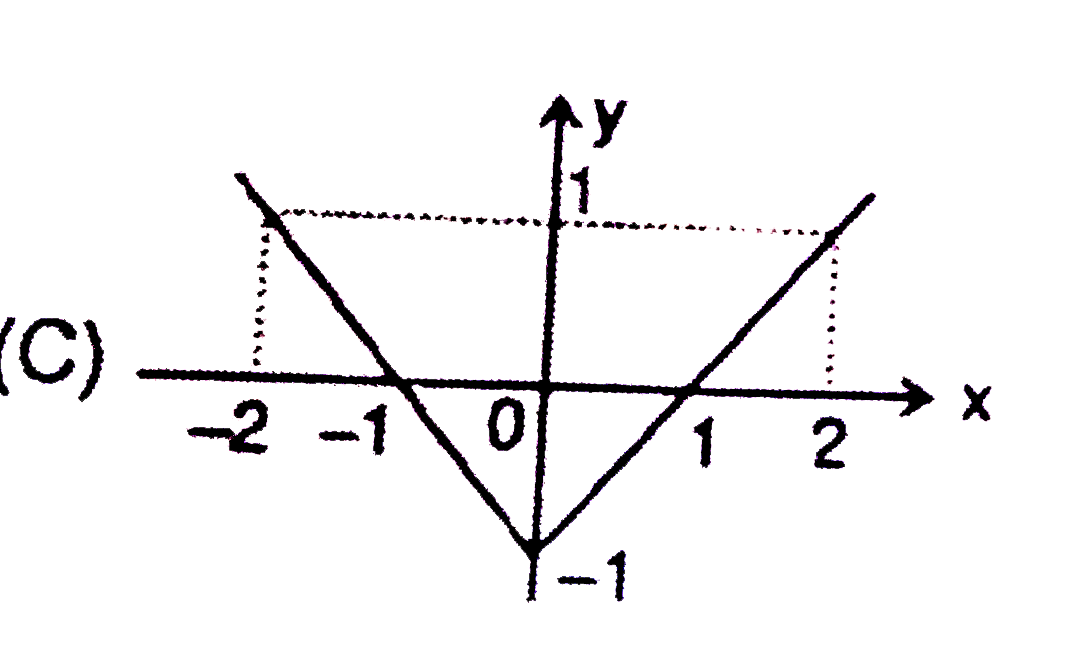 D
D
The absolute valued function f is defined as f(x)={xx≥0−xx<0} and fractional part function g(x) as g(x) = x-[x], graphically the number of real solution(s) of the equation f(x) = g(x) is obtained by finding the point(s) of interaction of the graph of y = f(x) and y = g(x).
The number of solutions (s) of |x−1|={x},x∈[−1,1] isA1B2C3DInfinitely many
The graph of the function y=f(x) is shown in the adjacent figure then correct statement is

View SolutionGraphical representation of different functions is also a method of find the number of solution (s) of any equation. The number of solution of the equation f1(x)=f2(x) is equal to the number of points of intersection of the graphs of y=f1(c)andy=f2(x). Now consider the equation
|x−1+|x−2|+|x−3∣=k. If k>2, then the number of solutions of the given equation is/are
View SolutionDraw the graph of the function f(x)=(1+1x)2
View SolutionDraw the graph of the solution set of the inequation 2x−y≥1
View SolutionThe absolute valued function f is defined as f(x)={xx≥0−xx<0} and fractional part function g(x) as g(x) = x-[x], graphically the number of real solution(s) of the equation f(x) = g(x) is obtained by finding the point(s) of interaction of the graph of y = f(x) and y = g(x).
The number of solution (s) |x−1|−|x+2|=k, when −3<k<3
View Solution

