Let ABC be a triangle and DandE be two points on side AB such that AD=BE. If DPBC and EQAC, THEN PROVE THAT PQAB.
In triangle ABC we have,
DP∣∣BC and EQ∣∣AC
Then, ADDB=APPC
BEEA=BQQC
= ADDB=APPC and ADDB=BQQC
⇒APPC=BQQC
In a △ABC, P and Q divide sides CA and CB respectively in the same ratio.
then PQ∣∣AB [By the converse of Basic Proportionality Theorem]
Topper's Solved these Questions
Similar Questions
ABCD is a trapezium in which ABDC . P and Q are points on sides AD and BC such that PQAB . If PD=18 , BQ=35 and QC=15 , find AD .
View SolutionABC is a triangle, P is a point on ABandQ is a point on AC such that ∠AQP=∠ABC. Complete the relation AreaofAPQAreaofABC=.()AC2 .
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
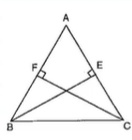
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960

View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn ABC , P and Q are points on sides AB and AC respectively such that PQBC . If AP=4cm, PB=6cm and PQ=3cm , determine BC .
View SolutionIn a ABC , P and Q are point on the sides AB and AC respectively, such that PQBC . If AP=2.4cm , AQ=2cm , QC=3cm and BC=6cm , find AB and PQ .
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
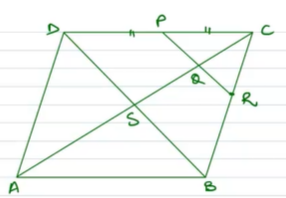
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View Solution
