In Figure, ABC is a right triangle right angled at B and points DandE trisect BC . Prove that 8AE2=3AC2+5AD2.
Since D and E are the points of trisection of BC,
therefore BD=DE=CE
Let BD=DE=CE=x
Then BE=2xandBC=3x
In right triangles ABD, ABE and ABC, (using Pythagoras theorem) We have,
(AD)2=(AB)2+(BD)2
⇒(AD)2=(AB)2+x2…(1)
(AE)2=(AB)2+(BE)2
⇒(AB)2+(2x)2
⇒(AE)2=(AB)2+4x2…(2)
And (AC)2=(AB)2+(BC)2=(AB)2+(3x)2
(AC)2=(AB)2+9x2
Now 8AE2–3AC2–5AD2=8(AB2+4x2)–3(AB2+9x2)–5(AB2+x2)=8AB2+32x2–3AB2–27x2–5AB2–5x2=0
8(AE)2–3(AC)2–5(AD)2=0
8(AE)2=3(AC)2+5(AD)2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a right angled triangle a2+b2+c2 is :
AR2B4R2C8R2Dnone of these
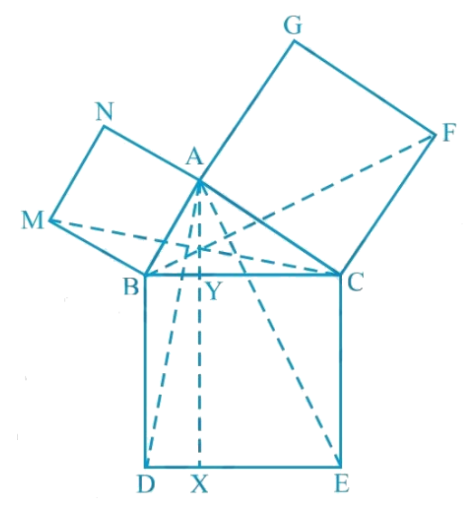
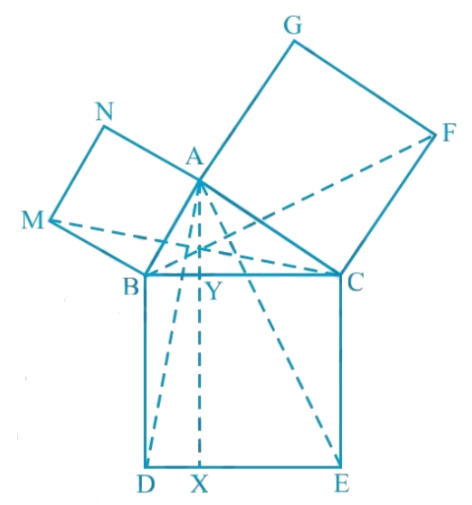
In Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)=2ar( FCB)
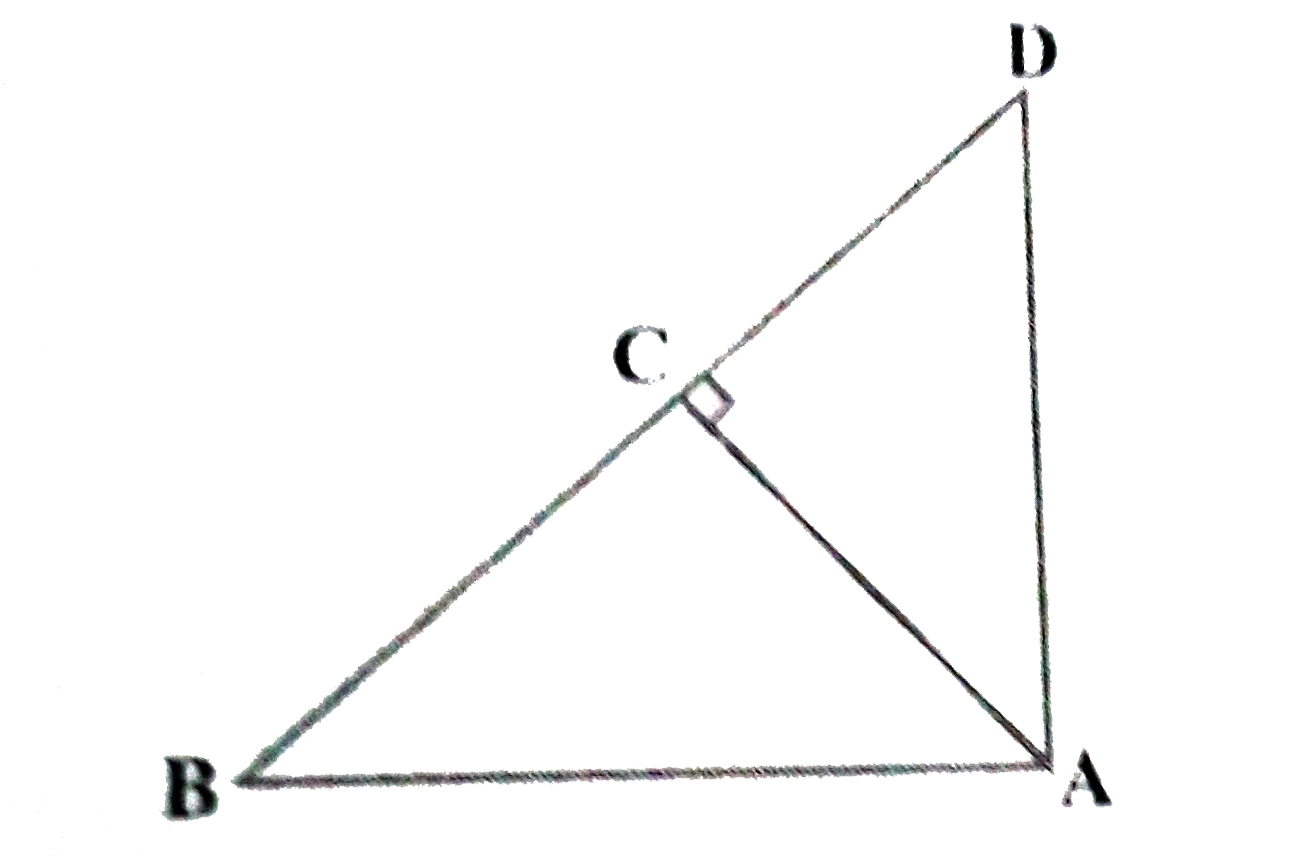
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
View SolutionIn fig.41, ABC is a right triangle right angled at A. D lies on BA produced and DE⊥BC, intersecting AC at F . if ∠AFE=1300, find ∠BDE (ii) ∠BCA ∠ABC
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
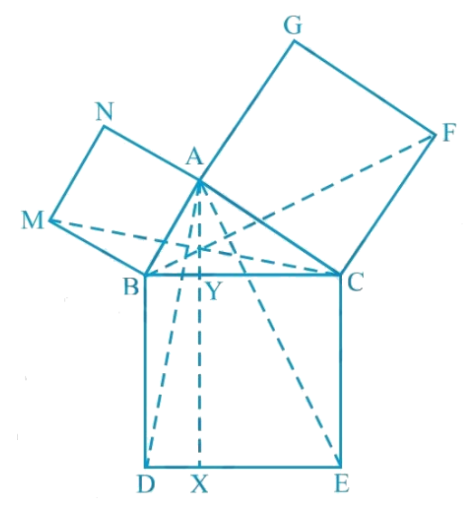
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=ar (ABMN)
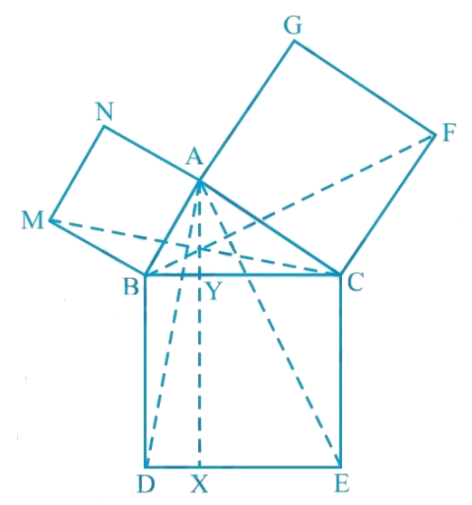
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)= ar (ACFG)
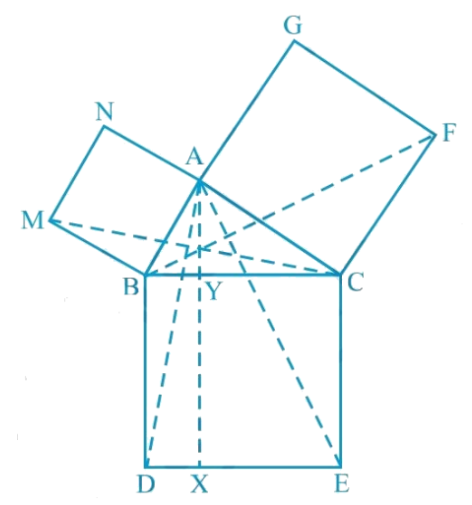
View Solution