Two triangles BACandBDC , right angled at AandD respectively, are drawn on the same base BC and on the same side of BC . If AC and DB intersect at P, prove that AP⋅PC=DP⋅PB.
Step by step video & image solution for Two triangles B A Ca n dB D C , right angled at Aa n dD respectively, are drawn on the same base B C and on the same side of B C . If A C and D B intersect at P , prove that A P*P C=D P*P Bdot by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two triangles BACandBDC , right angled at AandD respectively, are drawn on the same base BC and on the same side of BC . If AC and DB intersect at P, prove that AP⋅PC=DP⋅PB.
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View Solution
Knowledge Check
If the angles A,B,C of a triangle are in A.P. and sides a,b,c, are in G.P., then prove that a2,b2,c2 are in A.P.
AA.P.BH.P.CG.P.Dnone of these
ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD≅ACD (ii) ABP≅ACP AP bisects ∠A as well as ∠D AP is perpendicular bisector of BC.
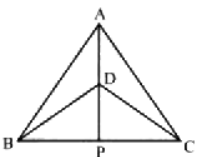
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionTwo triangle ABC and DBC lie on the same side of the base BC . From a point P on BC,PQAB AND PRBD ARE DRAWN. They meet AC in Q and DC in R respectively. Prove that QRAD.
View SolutionTriangles on the same base and between the same parallels are equal in area. GIVEN : Two triangles ABC and PBC on the same base BC and between the same parallel lines BC and AP. TO PROVE : ar(ABC)=ar(PBC) CONSTRUCTION : Through B, draw BDCA intersecting PA produced in D and through C, draw CQBP, intersecting line AP in Q.
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP

View SolutionABCD is a cyclic quadrilateral whose diagonals ACandBD intersect at P . If AB=DC, Prove that : PAB≅PDC PA=PDandPC=PB ADBC
View Solution