Question

Prove that the line segments joints joining the mid-points of the
adjacent sides of a quadrilateral from a parallelogram.

Explanation

To prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram, we will follow these steps:

Step 1: Identify the midpoints
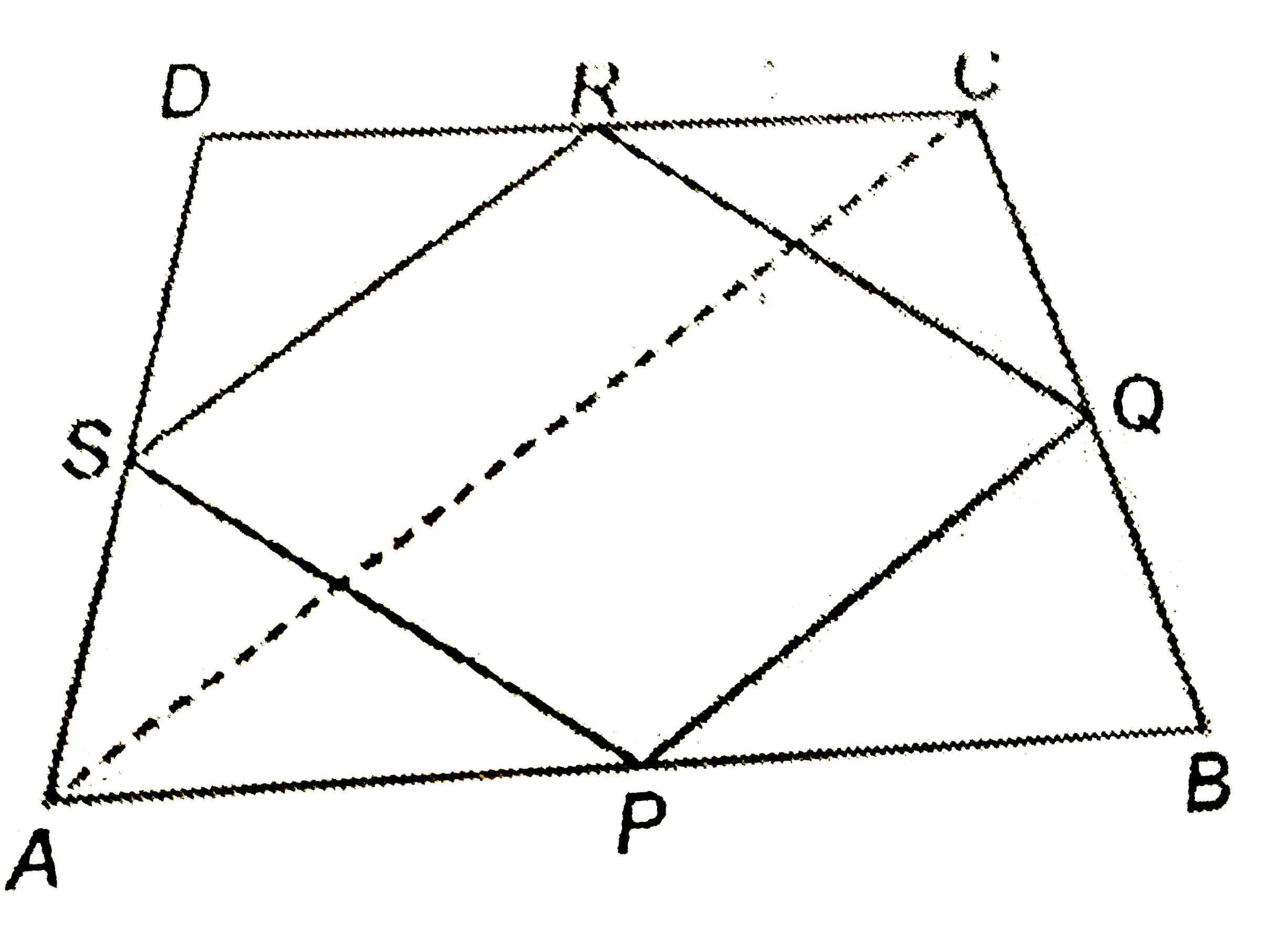
Let quadrilateral ABCD be given. We denote the midpoints of the sides as follows:
- P is the midpoint of side AB.
- Q is the midpoint of side BC.
- R is the midpoint of side CD.
- S is the midpoint of side AD.

Step 2: Draw the diagonals
Now, we will draw the diagonal AC of the quadrilateral ABCD.

Step 3: Analyze triangle ABC
In triangle ABC, since P and Q are the midpoints of sides AB and BC respectively, by the Midpoint Theorem, we can conclude that:
\( PQ \parallel AC \)
This means that the line segment PQ is parallel to the diagonal AC.

Step 4: Analyze triangle ADC
Next, we consider triangle ADC. Here, R and S are the midpoints of sides CD and AD respectively. Again, by the Midpoint Theorem, we can conclude that:
\( RS \parallel AC \)
This means that the line segment RS is also parallel to the diagonal AC.

Step 5: Establish parallelism between PQ and RS
Since both PQ and RS are parallel to AC, we can state that:
\( PQ \parallel RS \)

Step 6: Draw the other diagonal
Now, we will draw the diagonal BD of the quadrilateral ABCD.

Step 7: Analyze triangle ABD
In triangle ABD, P and S are the midpoints of sides AB and AD respectively. By the Midpoint Theorem, we can conclude that:
\( PS \parallel BD \)

Step 8: Analyze triangle BCD
In triangle BCD, Q and R are the midpoints of sides BC and CD respectively. By the Midpoint Theorem, we can conclude that:
\( QR \parallel BD \)

Step 9: Establish parallelism between PS and QR
Since both PS and QR are parallel to BD, we can state that:
\( PS \parallel QR \)

Step 10: Conclude that PQRS is a parallelogram
Now we have established that:
1. \( PQ \parallel RS \)
2. \( PS \parallel QR \)

Since both pairs of opposite sides are parallel, we conclude that quadrilateral PQRS is a parallelogram.

Final Conclusion
Thus, we have proved that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.

---