Two block of masses 1 kg 2 are connected by a metal wire going over a smooth pulley. The breaking stress of metal is 403π×106Mm−2 . What should be the minimum radius of wire used if it should not break?(g=10ms−2) Solution in Telugu
0.5mm
1mm
1.5mm
2mm
The correct Answer is:C
Breaking strength (or) Breaking stress
σ=FA=403π×106N/m2
3×10πr2=403π×106
∴r=1.5×10−3m=1.5mm
Topper's Solved these Questions
Similar Questions
A circular loop and a square loop are formed from two wires of same length and cross section. Same current is passed through them. Then the ratio of their dipole moments is
View SolutionThe dimensions of a/b in the equation p=a−t2bx where P is pressure, x is distance ant 't' is time are,
View SolutionTwo blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109m−2. What should be the minmum radius of the wire used if it is not to break? Take g=10ms−2
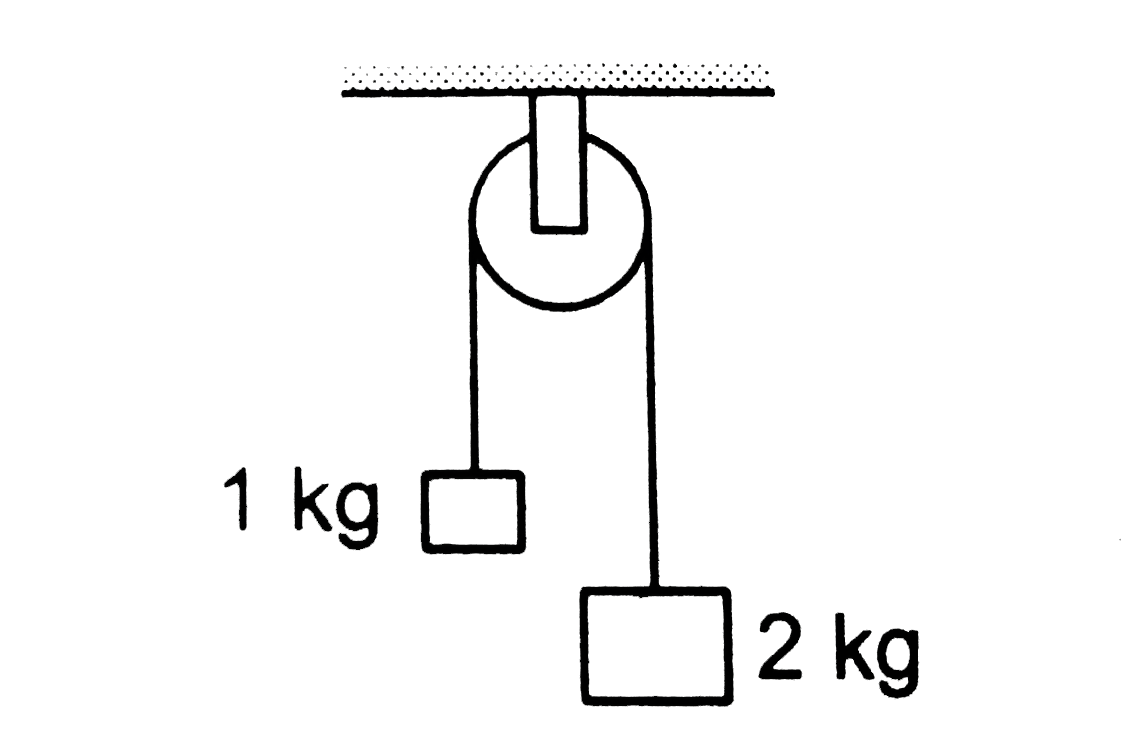
View SolutionTwo blocks of masses 1 kg and 2 kg are connected by a metal wire goijng over a smooth pulley as shown in figure. The breaking stress of the metal is (40//3pi)xx10^(6)N//m^(2) . If g=10ms^(-12) , then what should be the minimum radlus of the wire used if it is not to break?
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
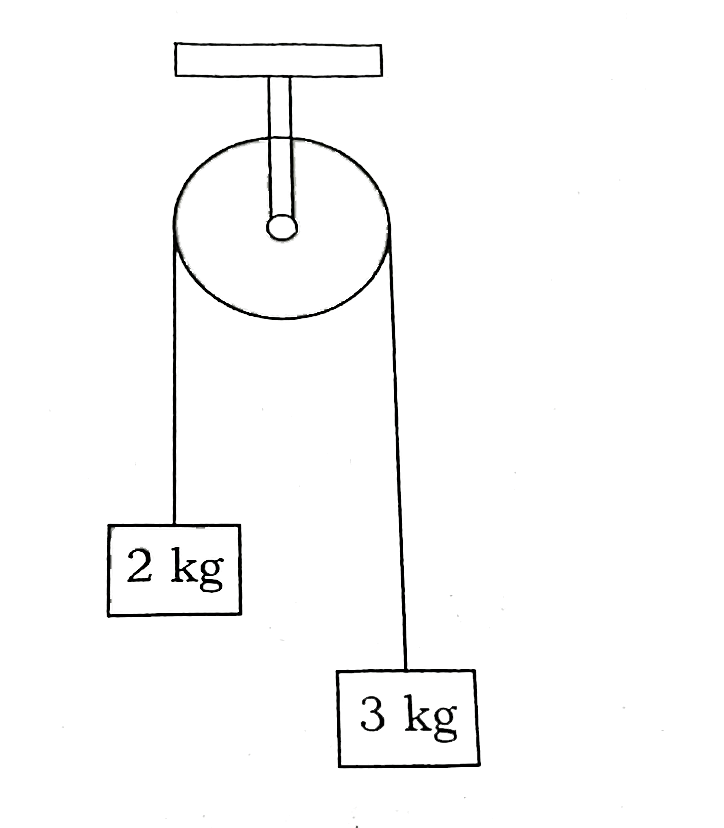
View SolutionTwo blocks of masses 1 kg and 2 kg are connected by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109Nm−2. What should be the minimum radius of the wire used if it is not to break?
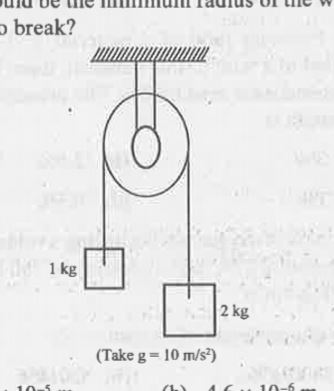
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2xx10^(9)"N m"^(-2) . If g=10ms^(-2) , then what is the minimum radius of the wire which will not break
View SolutionTwo blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109Nm−2. What should be the minimum radius of the wire used if it is not to break? Take g=10ms−2
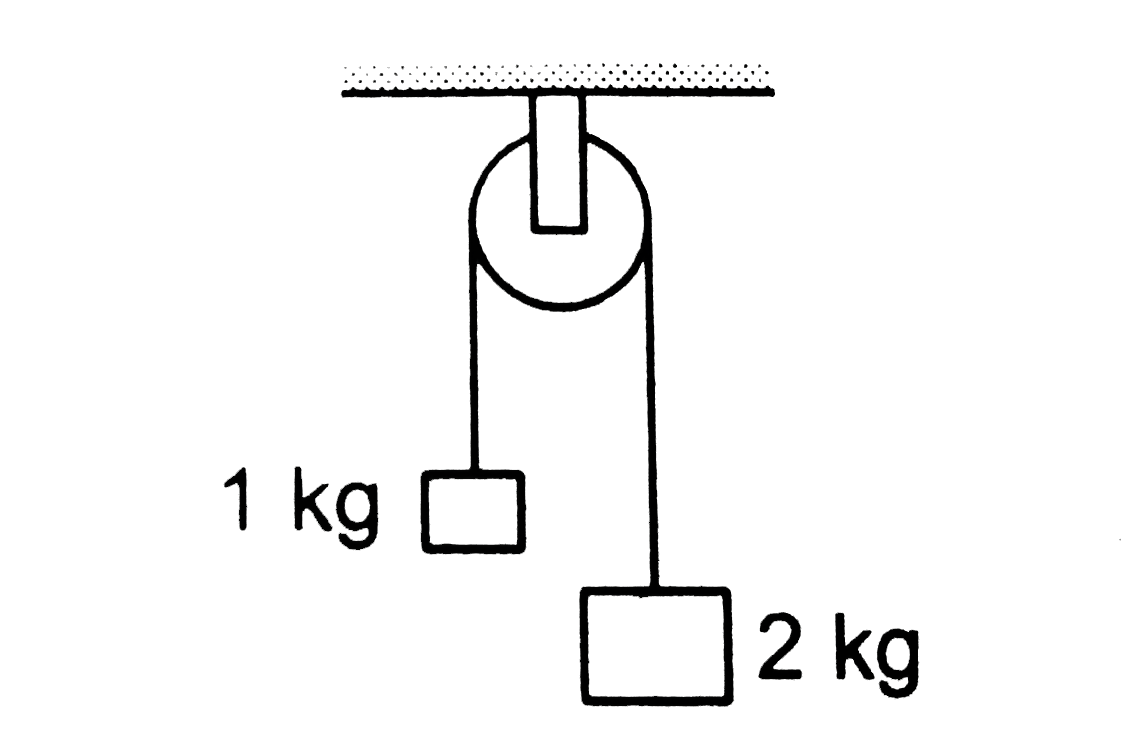
View SolutionTwo block of masses 1 kg 2 are connected by a metal wire going over a smooth pulley. The breaking stress of metal is 403π×106Mm−2 . What should be the minimum radius of wire used if it should not break?(g=10ms−2)
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
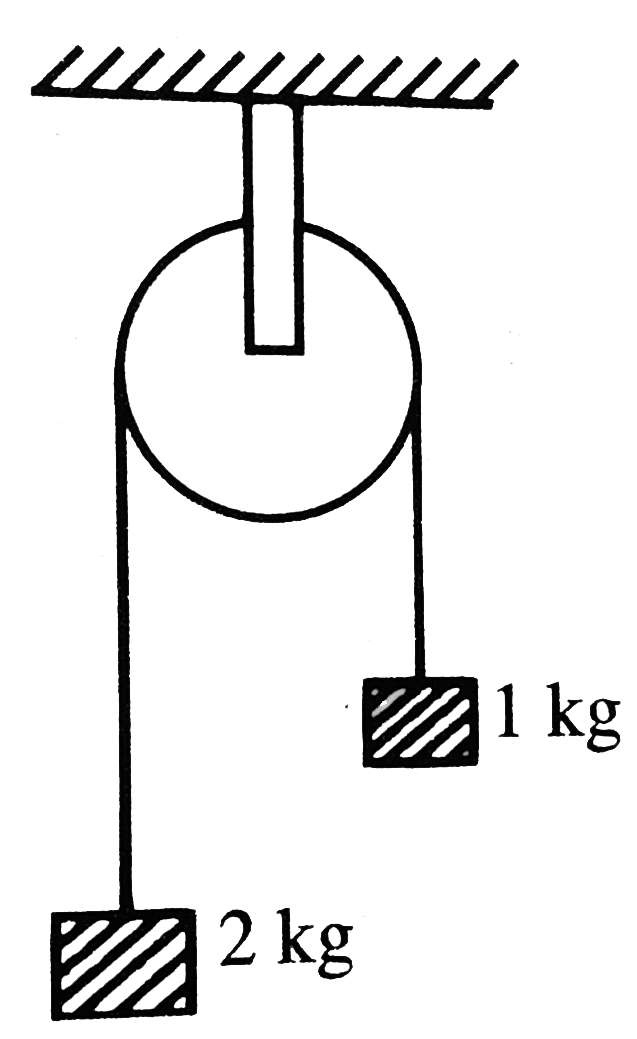
View SolutionTwo block of masses 1 kg 2 are connected by a metal wire going over a smooth pulley. The breaking stress of metal is 403π×106Mm−2 . What should be the minimum radius of wire used if it should not break?(g=10ms−2)
View SolutionTwo blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2xx10^(9)Nm^(-2) . What would be the minimum radius of the wire used if it not to break ? Take , g=10 ms^(-2)
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?

View SolutionTwo masses 7 kg and 12 kg are connected at the two ends of a metal wire that goes ove a frictionless puulley. What should be in the minimum radius of the wire in order that the wire does not break,if the breaking stess of the metal is 1.3×108N/m2 ?
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2xx10^(9)"N m"^(-2) . If g=10ms^(-2) , then what is the minimum radius of the wire which will not break
View Solution
